题目内容
在△ABC中,三个内角A,B,C的对边分别为a,b,c,若a=2
,c=2,A=120°,S△ABC= .
| 3 |
考点:正弦定理
专题:解三角形
分析:由正弦定理和已知易得C=30°,进而可得sinB=
,由三角形的面积公式可得.
| 1 |
| 2 |
解答:
解:∵在△ABC中,a=2
,c=2,A=120°,
∴由正弦定理可得sinC=
=
=
,
∴C=30°,或C=150°(A=120°,应舍去),
∴sinB=sin(A+C)=sin150°=
∴S△ABC=
acsinB=
×2
×2×
=
故答案为:
| 3 |
∴由正弦定理可得sinC=
| csinA |
| a |
2×
| ||||
2
|
| 1 |
| 2 |
∴C=30°,或C=150°(A=120°,应舍去),
∴sinB=sin(A+C)=sin150°=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
故答案为:
| 3 |
点评:本题考查正弦定理,涉及三角形的面积公式,属基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
若函数y=f(x)唯一的一个零点同时在区间(0,2),(1,2),(0,4),则下列命题中正确的是( )
| A、函数f(x)在区间(0,1)内有零点 |
| B、函数f(x)在区间(1,1.5)内有零点 |
| C、函数f(x)在区间(2,4)内无零点 |
| D、函数f(x)在区间(1,4)内无零点 |
函数y=Asin(ωx+φ)图象的一部分如图所示,则此函数的解析式可以写成( )
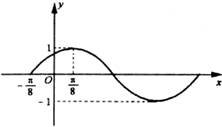

A、y=sin(2x+
| ||
B、y=sin(x+
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|