题目内容
20.函数f(x)=lg(3x+3-x-a)的值域是R,则a的取值范围是a≥2.分析 若函数f(x)=lg(3x+3-x-a)的值域是R,则真数部分3x+3-x-a的最小值2-a≤0,进而得到答案.
解答 解:∵函数f(x)=lg(3x+3-x-a)的值域是R,
故3x+3-x-a的最小值2-a≤0,
解得:a≥2,
故答案为:a≥2.
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的两点A,B,若|AF|=4|FB|,则k的值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{3}{4}\sqrt{2}$ | C. | $\frac{{\sqrt{17}}}{4}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
10.已知直线l与抛物线y2=4x相切于点M,与其准线相交于点N,以MN为直径的圆过x轴上一个定点P,则定点P的坐标为( )
| A. | (-1,0) | B. | (1,0) | C. | (2,0) | D. | (4,0) |
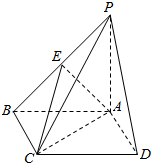 在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,E为PB的中点.
在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,E为PB的中点.