题目内容
10.已知直线l与抛物线y2=4x相切于点M,与其准线相交于点N,以MN为直径的圆过x轴上一个定点P,则定点P的坐标为( )| A. | (-1,0) | B. | (1,0) | C. | (2,0) | D. | (4,0) |
分析 求出切线方程,确定M,N的坐标,验证$\overrightarrow{MF}$•$\overrightarrow{NF}$=0,即可得出结论.
解答 解:设M($\frac{{{y}_{0}}^{2}}{4}$,y0)(y0>0),y=2$\sqrt{x}$,则y′=$\frac{1}{\sqrt{x}}$,
∴直线l的方程为y-y0=$\frac{2}{{y}_{0}}$(x-$\frac{{{y}_{0}}^{2}}{4}$),
设x=-1,则y=-$\frac{2}{{y}_{0}}$+$\frac{{y}_{0}}{2}$,
∴$\overrightarrow{MF}$•$\overrightarrow{NF}$=(1-$\frac{{{y}_{0}}^{2}}{4}$,-y0)•(2,$\frac{2}{{y}_{0}}$-$\frac{{y}_{0}}{2}$)=2-$\frac{{{y}_{0}}^{2}}{2}$-2+$\frac{{{y}_{0}}^{2}}{2}$=0,
∴MF⊥NF,
∴以MN为直径的圆过x轴上一个定点P(1,0),
故选:B.
点评 本题考查抛物线的方程与性质,考查向量知识的运用,属于中档题.

练习册系列答案
相关题目
5.给出下列三个问题:
①从高二(3)班60名学生中,抽出8名学生去参加座谈
②将全年级学号尾数为5的同学的作业收来检查
③甲乙丙三个车间生产了同一种产品分别为60件,40件、30件,为了解产品质量,取一个容量为13的样本调查
则以上问题适宜采用的抽样方法分别是( )
①从高二(3)班60名学生中,抽出8名学生去参加座谈
②将全年级学号尾数为5的同学的作业收来检查
③甲乙丙三个车间生产了同一种产品分别为60件,40件、30件,为了解产品质量,取一个容量为13的样本调查
则以上问题适宜采用的抽样方法分别是( )
| A. | 简单随机抽样、系统抽样、分层抽样 | B. | 简单随机抽样、分层抽样、系统抽样 | ||
| C. | 系统抽样、分层抽样、简单随机抽样 | D. | 系统抽样、简单随机抽样、分层抽样 |
15.“存在x∈Z,使2x+m≤0”的否定是( )
| A. | 存在x∈Z,使2x+m>0 | B. | 不存在x∈Z,使2x+m>0 | ||
| C. | 对任意x∈Z,都有2x+m≤0 | D. | 对任意x∈Z,都有2x+m>0 |
19.下列函数是偶函数的是( )
| A. | $y=\frac{1}{x}+x$ | B. | y=x3 | C. | $y=\sqrt{x}$ | D. | y=x2+1 |
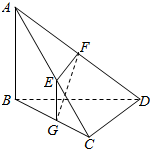 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证:
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证: