题目内容
12.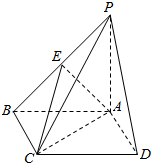 在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,E为PB的中点.
在如图所示的四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,E为PB的中点.(Ⅰ)求证:PD∥平面ACE;
(Ⅱ)求证:PC⊥AE.
分析 (Ⅰ)连接BD交AC与O,连接EO,可得OE∥PD,又OE?平面ACE,PD?平面ACE,即可判定PD∥平面ACE.
(Ⅱ)先证明PA⊥BC,CB⊥AB,可得CB⊥平面PAB,可得CB⊥AE,又AE⊥PB,即可证明AE⊥平面PBC,从而可证PC⊥AE.
解答 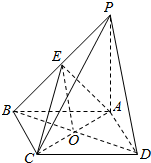 (本题满分为12分)证明:(Ⅰ)连接BD交AC与O,连接EO,
(本题满分为12分)证明:(Ⅰ)连接BD交AC与O,连接EO,
∵E,O分别为BP,BD的中点,
∴OE∥PD,
又∵OE?平面ACE,PD?平面ACE,
∴PD∥平面ACE.…4分
(Ⅱ)∵PA⊥平面ABCD,BC?平面ABCD,
∴PA⊥BC,…6分
又∵底面ABCD是矩形,
∴CB⊥AB,
∵PA∩AB=A,
∴CB⊥平面PAB,…8分
又∵AE?平面PAB,
∴CB⊥AE,
又∵PA=AB,E为PB的中点,
∴AE⊥PB,…10分
∵PB∩BC=B,
∴AE⊥平面PBC,
又∵PC?平面PBC,
∴PC⊥AE.…12分
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的判定和性质,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
4.函数f(x)=2x的图象在x=0处的切线方程是( )
| A. | y=x+1 | B. | y=2x+1 | C. | y=xln2-1 | D. | y=xln2+1 |
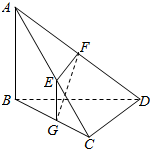 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证:
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证: