题目内容
16.设等差数列{an}前n项和为Sn,则有以下性质:Sk,S2k-Sk,S3k-S2k,S4k-S3k(k≠1)成等差数列(1)类比等差数列的上述性质,写出等比数列{bn}前n项积Tn的类似性质;
(2)证明(1)中所得结论.
分析 (1)类比等差数列的上述性质,可得等比数列{bn}前n项积Tn的类似性质:Tk,T2k-Tk,T3k-T2k,T4k-T3k(k≠1)成等比数列.
(2)设等比数列{bn}的公比为q,可得Tk=b1+b2+…+bk,T2k-Tk=bk+1+bk+2+…+b2k=qkTk,同理可得:T3k-T2k=qk(T3k-T2k),T4k-T3k=qk(T3k-T2k).即可证明.
解答 (1)解:类比等差数列的上述性质,可得等比数列{bn}前n项积Tn的类似性质:Tk,T2k-Tk,T3k-T2k,T4k-T3k(k≠1)成等比数列.
(2)证明:设等比数列{bn}的公比为q,
则Tk=b1+b2+…+bk,
T2k-Tk=bk+1+bk+2+…+b2k=qk(b1+b2+…+bk)=qkTk,
同理可得:T3k-T2k=qk(T3k-T2k),
T4k-T3k=qk(T3k-T2k).
∴Tk,T2k-Tk,T3k-T2k,T4k-T3k(k≠1)成等比数列.
点评 本题考查了等差数列与等比数列的通项公式性质及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
6.若圆锥的侧面展开图的圆心角为90°,半径为r,则该圆锥的全面积为( )
| A. | $\frac{π{r}^{2}}{16}$ | B. | $\frac{3π{r}^{2}}{16}$ | C. | $\frac{π{r}^{2}}{4}$ | D. | $\frac{5π{r}^{2}}{16}$ |
4.已知某几何体的三视图如图所示,则该几何体的表面积为( )
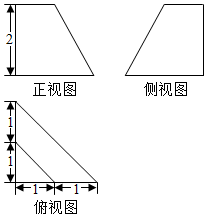

| A. | $\frac{7}{3}$ | B. | $\frac{17}{2}$ | C. | 13 | D. | $\frac{17+3\sqrt{10}}{2}$ |
1.在△ABC中,若a=$\sqrt{3}$,b=1,c=2,则△ABC的面积等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
5.函数y=$\root{3}{{x}^{2}}$-x2+2的图象在以点(1,y1)为切点的切线与坐标轴所围成的三角形面积等于( ),函数y=x3图象上过点(1,y2)的切线与两条坐标轴所围成的三角形面积等于( )
| A. | $\frac{25}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{1}{24}$ | D. | $\frac{15}{4}$ | ||||
| E. | $\frac{7}{3}$ | F. | $\frac{15}{4}$或$\frac{7}{3}$ |
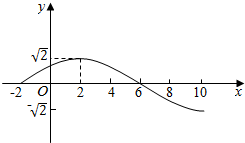 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$).