题目内容
已知函数f(x)=a(x-1)3+bx+c(a∈R,b,c∈Z),对于取定的一组a,b,c的值,若计算得到f(-1)=2,则f(3)的值一定不能等于( )
| A、4 | B、3 | C、2 | D、0 |
考点:函数的值
专题:函数的性质及应用
分析:由已知求出f(-1)和f(3),由b,c∈Z,得f(-1)+f(3)的值为偶数,由此根据f(-1)=2,得到f(3)的值一定不能是奇数.
解答:
解:∵函数f(x)=a(x-1)3+bx+c(a∈R,b,c∈Z),对于取定的一组a,b,c的值,若计算得到f(-1)=2,
∴f(-1)=-8a-b+c,f(3)=8a+3b+c,
∴f(-1)+f(3)=2(b+c),
∵b,c∈Z,∴f(-1)+f(3)的值为偶数,
∵f(-1)=2,∴f(3)的值一定不能是奇数,
故选:B.
∴f(-1)=-8a-b+c,f(3)=8a+3b+c,
∴f(-1)+f(3)=2(b+c),
∵b,c∈Z,∴f(-1)+f(3)的值为偶数,
∵f(-1)=2,∴f(3)的值一定不能是奇数,
故选:B.
点评:本题考查函数值的求法,是基础题,解题时要注意函数性质的合理运用.

练习册系列答案
相关题目
函数y=-xsinx在[-π,π]上的图象是( )
A、 |
B、 |
C、 |
D、 |
从2014名学生中选取50名组成参观团,若采用下面的方法选取:先用简单随机抽样从2014人中剔除14人,剩下2000人再按系统抽样的方法进行,则每人入选的概率( )
| A、不全相等 | ||
| B、均不相等 | ||
C、都相等且为
| ||
D、都相等且为
|
在等差数列{an}中,已知a2=3,a5=9,则数列{an}的公差d为( )
| A、1 | B、-1 | C、2 | D、-2 |
 已知函数f(x)=Asin(ωx+φ)(A,ω>0)的部分图象如图所示.(1)求函数f(x)的解析式(2)若集合{x|f(x)=m},x∈[0,
已知函数f(x)=Asin(ωx+φ)(A,ω>0)的部分图象如图所示.(1)求函数f(x)的解析式(2)若集合{x|f(x)=m},x∈[0,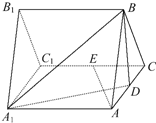 如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.
如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.