题目内容
4.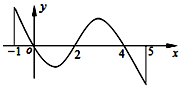 已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.
已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
①函数f(x)的极大值点有2个;
②函数f(x)在[0,2]上是减函数;
③若x∈[-1,t]时,f(x)的最大值是2,则t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中是真命题的是①②.(填写序号)
分析 先由导函数的图象和原函数的关系画出原函数的大致图象,再借助与图象和导函数的图象,对四个命题,一一进行验证,对于假命题采用举反例的方法进行排除即可得到答案.
解答 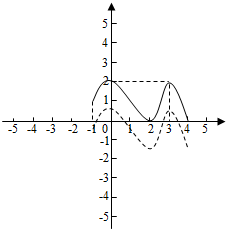 解:由导函数的图象和原函数的关系得,原函数的大致图象如图:
解:由导函数的图象和原函数的关系得,原函数的大致图象如图:
由图得:∵f(x)的极大值点有2个,故①为真命题;
②为真命题.因为在[0,2]上导函数为负,故原函数递减;
由已知中y=f′(x)的图象,及表中数据可得当x=0或x=4时,函数取最大值2,
若x∈[-1,t]时,f(x)的最大值是2,那么0≤t≤5,故t的最大值为5,即③错误;
④由于f(3)未知,故当1<a<2时,函数y=f(x)-a有4个零点,不正确.
故答案为①②.
点评 本题主要考查导函数和原函数的单调性之间的关系.二者之间的关系是:导函数为正,原函数递增;导函数为负,原函数递减.

练习册系列答案
相关题目
14.在y=sin|x|,y=|sinx|,y=sin(2x+$\frac{2π}{3}$),y=cos($\frac{x}{2}$+$\frac{2π}{3}$),y=cosx+|cosx|$y=tan\frac{1}{2}x+1$中,最小正周期为π的函数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.某三棱锥的三视图如图所示,则该三棱锥外接球的表面积为( )


| A. | 5π | B. | 25π | C. | 50π | D. | 100π |
19.已知集合A={x|log2x≤1},B={x|$\frac{1}{x}$>1},则A∩(∁RB)=( )
| A. | (-∞,2] | B. | (0,1] | C. | [1,2] | D. | (2,+∞) |
9.某几何体的三视图如图所示(单位:cm),则该几何体的侧面PAB的面积是( )
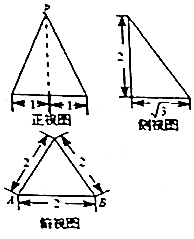

| A. | $\sqrt{7}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}$ |
16.关于下面等高条形图说法正确的有( )
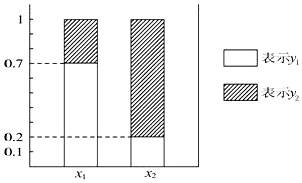

| A. | 在被调查的 x 1中,y 1占70% | B. | 在被调查的 x 2中,y 2占20% | ||
| C. | x 1与 y 1有关 | D. | 以上都不对 |
 如图所示,在△ABC中,I为△ABC的内心,AI交BC于D,交△ABC外接圆于E
如图所示,在△ABC中,I为△ABC的内心,AI交BC于D,交△ABC外接圆于E