题目内容
在平面直角坐标系xOy中,已知抛物线C:x2=4y的焦点为F,定点A(2
,0),若射线FA与抛物线C相交于点M,与抛物线C的准线相交于点N,则FM:MN= .
| 2 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出抛物线C的焦点F的坐标,从而得到AF的斜率k=-
,过M作MP⊥l于P,根据抛物线物定义得FM=PM.Rt△MPN中,根据tan∠MNP=
,从而得到PN=2
PM,进而算出MN=3PM,由此即可得到FM:MN的值.
| ||
| 4 |
| ||
| 4 |
| 2 |
解答:
解:∵抛物线C:x2=4y的焦点为F(0,1),点A坐标为(2
,0),
∴抛物线的准线方程为l:y=-1,直线AF的斜率为k=
=-
,
过M作MP⊥l于P,根据抛物线物定义得FM=PM,
∵Rt△MPN中,tan∠MNP=-k=
,
∴
=
,可得PN=2
PM,
得MN=3PM
因此可得FM:MN=PM:MN=1:3.
故答案为:1:3.
| 2 |
∴抛物线的准线方程为l:y=-1,直线AF的斜率为k=
| 0-1 | ||
2
|
| ||
| 4 |
过M作MP⊥l于P,根据抛物线物定义得FM=PM,
∵Rt△MPN中,tan∠MNP=-k=
| ||
| 4 |
∴
| PM |
| PN |
| ||
| 4 |
| 2 |
得MN=3PM
因此可得FM:MN=PM:MN=1:3.
故答案为:1:3.
点评:本题给出抛物线方程和射线FA,求线段的比值.着重考查了直线的斜率、抛物线的定义、标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知点A、B、C、D均在球O上,AB=BC=
,AC=3,若三棱锥D-ABC体积的最大值为
,则球O的表面积为( )
| 3 |
3
| ||
| 4 |
| A、36π | ||
| B、16π | ||
| C、12π | ||
D、
|
已知非零向量
,
,则“|
-
|=|
|+|
|”是“
+2
=
”成立的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 0 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
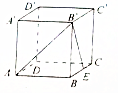 如图所示,在棱长为1的正方体ABCD-A′B′C′D′中,E为棱BC的中点.
如图所示,在棱长为1的正方体ABCD-A′B′C′D′中,E为棱BC的中点. 如图,⊙O的半径OC垂直于直径DB,F为BO上一点,CF的延长线交⊙O于点E,过E点的切线交DB的延长线于点A
如图,⊙O的半径OC垂直于直径DB,F为BO上一点,CF的延长线交⊙O于点E,过E点的切线交DB的延长线于点A 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2.
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2. 已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为菱形,且∠DAB=
已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为菱形,且∠DAB=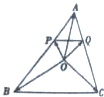 如图,O是△ABC内一点,PQ∥BC,且
如图,O是△ABC内一点,PQ∥BC,且