Question

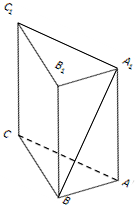如图，已知三棱柱ABC-A₁B₁C₁的六个顶点都在球O的球面上，若AA₁⊥平面A₁B₁C₁，A₁B₁⊥B₁C₁，AA₁=8，A₁B₁=6，A₁C₁=2

34

，则球O的体积为

 

．

Answer 1

考点：球的体积和表面积

专题：计算题,空间位置关系与距离

分析：因为三棱柱ABC-A₁B₁C₁中，AA₁⊥平面A₁B₁C₁，A₁B₁⊥B₁C₁，所以三棱柱的底面是直角三角形，侧棱与底面垂直，侧面A₁ACC₁，经过球的球心，球的直径是其对角线的长，求出球的半径，即可求出球O的体积．

解答： 解：因为三棱柱ABC-A₁B₁C₁中，AA₁⊥平面A₁B₁C₁，A₁B₁⊥B₁C₁，所以三棱柱的底面是直角三角形，侧棱与底面垂直，侧面A₁ACC₁，经过球的球心，球的直径是其对角线的长，
因为AA₁=8，A₁C₁=2

34

，所以AC₁=

64+136

=10

2

，所以球的半径为：5

2

，
所以球O的体积为

4

3

π×(5

2

)3=

1000 2

3

π．
故答案为：

1000 2

3

π．

点评：本题考查球O的体积，考查学生的计算能力，求出球的半径是关键．