题目内容
已知数列{an},
(1)a1=1,an=an-1+2n-1(n≥2),则an=
(2)若a1=1,an+1=
an,则an=
(3)若a1=1,an=2an-1+1(n≥2),则an=
(4)若前n项和Sn=3n2+n+1,则an=
(5)若a1=
,Sn=n2an,则an= .
(1)a1=1,an=an-1+2n-1(n≥2),则an=
(2)若a1=1,an+1=
| n |
| n+1 |
(3)若a1=1,an=2an-1+1(n≥2),则an=
(4)若前n项和Sn=3n2+n+1,则an=
(5)若a1=
| 1 |
| 2 |
考点:数列递推式
专题:等差数列与等比数列
分析:(1)采用叠加法求数列的通项公式.
(2)采用叠乘法求数列的通项公式.
(3)采用构造新数列法求数列的通项公式.
(4)采用前n项和法求数列的通项公式.
(5)采用前n项和与叠乘法求数列的通项公式.
(2)采用叠乘法求数列的通项公式.
(3)采用构造新数列法求数列的通项公式.
(4)采用前n项和法求数列的通项公式.
(5)采用前n项和与叠乘法求数列的通项公式.
解答:
解:(1)a1=1,an=an-1+2n-1(n≥2),
则:an-an-1=2n-1
an-1-an-2=2(n-1)-1
…
a2-a1=2•2-1
所以:an-a1=2(2+3+…+n)-n
an=2•
-2-n+1
整理得:an=n2-1
(2)a1=1,an+1=
an,
则:
=
=
…
=
所以:
=
解得:an=
(3)a1=1,an=2an-1+1(n≥2),
则:
=2,所以数列{an+1}是以a1+1为首项,公比为2的等比数列.
an+1=(a1+1)2n-1
则:an=2n-1当n=1时符合此通项公式
所以:an=2n-1
(4)数列前n项和Sn=3n2+n+1,
则:Sn-1=3(n-1)2+(n-1)+1(n≥2)
an=Sn-Sn-1=6n-2
a1=5,不符合此通项公式,
所以:an=
(5)a1=
,Sn=n2an,①
则Sn-1=(n-1)2an-1②
①-②得:
=
则:采用(2)的方法
即得:an=
则:an-an-1=2n-1
an-1-an-2=2(n-1)-1
…
a2-a1=2•2-1
所以:an-a1=2(2+3+…+n)-n
an=2•
| n(n+1) |
| 2 |
整理得:an=n2-1
(2)a1=1,an+1=
| n |
| n+1 |
则:
| an |
| an-1 |
| n-1 |
| n |
| an-1 |
| an-2 |
| n-2 |
| n-1 |
…
| a2 |
| a1 |
| 1 |
| 2 |
所以:
| an |
| a1 |
| 1 |
| n |
解得:an=
| 1 |
| n |
(3)a1=1,an=2an-1+1(n≥2),
则:
| an+1 |
| an-1+1 |
an+1=(a1+1)2n-1
则:an=2n-1当n=1时符合此通项公式
所以:an=2n-1
(4)数列前n项和Sn=3n2+n+1,
则:Sn-1=3(n-1)2+(n-1)+1(n≥2)
an=Sn-Sn-1=6n-2
a1=5,不符合此通项公式,
所以:an=
|
(5)a1=
| 1 |
| 2 |
则Sn-1=(n-1)2an-1②
①-②得:
| an |
| an-1 |
| n-1 |
| n+1 |
则:采用(2)的方法
即得:an=
| 1 |
| n(n+1) |
点评:本题考查的知识要点:利用叠加和叠乘法,前n项和法求数列的通项公式,属于基础题型.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
已知椭圆的标准方程x2+
=1,则椭圆的焦点坐标为( )
| y2 |
| 10 |
A、(±
| ||
B、(0,±
| ||
| C、(0,±3) | ||
| D、(±3,0) |
定义行列式运算:
=a1a4-a2a3,将函数f(x)=
(ω>0)的图象向左平移
个单位,所得图象对应的函数为偶函数,则ω的最小值是( )
|
|
| 5π |
| 6 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
如果实数x,y满足
,则
的最大值为( )
|
| 4x+2y-16 |
| x-3 |
A、
| ||
| B、6 | ||
| C、7 | ||
| D、8 |
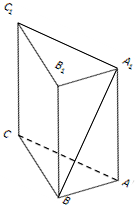 如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2