题目内容
一动圆与两圆:x2+y2+4x+3=0和x2+y2-4x-5=0都外切,则动圆的圆心M的轨迹方程是 .
考点:轨迹方程,圆与圆的位置关系及其判定
专题:直线与圆
分析:设所求圆的圆心坐标M(x,y),半径为r,由所求圆与两个圆都外切,可得|PC1|=r+1,|PC2|=r+3,即|MC2|-|MC1|=2,根据双曲线定义可知P点的轨迹为以C1,C2为焦点的双曲线,从而求得圆心M的轨迹方程.
解答:
解:x2+y2+4x+3=0即 (x+2)2+y2 =1,(x-2)2+y2 =9,
故两圆的圆心分别是C1(-2,0)、C2(2,0),半径分别为1和3.
设所求圆的圆心坐标M(x,y),半径为r,
∵所求圆与两个圆都外切,∴|PC1|=r+1,|PC2|=r+3,
即|MC2|-|MC1|=2,
根据双曲线定义可知P点的轨迹为以C1,C2为焦点的双曲线,
故有c=2;2a=2,a=1,b=
=
,
故圆心M的轨迹方程是 x2-3y2=1,
故答案为:x2-3y2=1.
故两圆的圆心分别是C1(-2,0)、C2(2,0),半径分别为1和3.
设所求圆的圆心坐标M(x,y),半径为r,
∵所求圆与两个圆都外切,∴|PC1|=r+1,|PC2|=r+3,
即|MC2|-|MC1|=2,
根据双曲线定义可知P点的轨迹为以C1,C2为焦点的双曲线,
故有c=2;2a=2,a=1,b=
| c2-a2 |
| 3 |
故圆心M的轨迹方程是 x2-3y2=1,
故答案为:x2-3y2=1.
点评:本题主要考查圆的标准方程,圆和圆相切的性质,双曲线的定义,属于基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
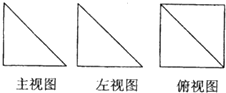 一个几何体的三视图如图所示,其中正视图和侧(左)视图是腰长为4的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧(左)视图是腰长为4的两个全等的等腰直角三角形,则该几何体的体积为( )| A、16 | ||
| B、64 | ||
C、
| ||
D、
|
定义行列式运算:
=a1a4-a2a3,将函数f(x)=
(ω>0)的图象向左平移
个单位,所得图象对应的函数为偶函数,则ω的最小值是( )
|
|
| 5π |
| 6 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
设p:(x-2)(y-5)≠0;q:x≠2或y≠5,则p是q的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
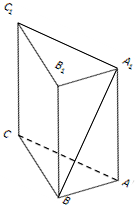 如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2