题目内容
若直线(3λ+1)x+(1-λ)y+6-6λ=0与不等式组
表示的平面区域有公共点,则实数λ的取值范围是( )
|
A、(-∞,-
| ||
B、,(-
| ||
| C、(1,9) | ||
D、(-∞,-
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用线性规划的知识即可得到结论.
解答:
解:(3λ+1)x+(1-λ)y+6-6λ=0等价为λ(3x-y-6)+(x+y+6)=0,
则
,解得
,即直线过定点D(0,-6)
作出不等式组对应的平面区域如图: 其中A(2,1),B(5,2),
其中A(2,1),B(5,2),
此时AD的斜率k=
=
,BD的斜率k=
=
,
当直线过A时,λ=9,
当直线过B时,λ=-
,
则若直线(3λ+1)x+(1-λ)y+6-6λ=0与不等式组
表示的平面区域有公共点,
则满足直线的斜率
≤
≤
,
解得λ∈(-∞,-
)∪(9,+∞),
故选:A
则
|
|
作出不等式组对应的平面区域如图:
 其中A(2,1),B(5,2),
其中A(2,1),B(5,2),此时AD的斜率k=
| -6-1 |
| 0-2 |
| 7 |
| 2 |
| -6-2 |
| 0-5 |
| 8 |
| 5 |
当直线过A时,λ=9,
当直线过B时,λ=-
| 13 |
| 7 |
则若直线(3λ+1)x+(1-λ)y+6-6λ=0与不等式组
|
则满足直线的斜率
| 8 |
| 5 |
| 3λ+1 |
| λ-1 |
| 7 |
| 2 |
解得λ∈(-∞,-
| 13 |
| 7 |
故选:A
点评:本题主要考查线性规划的应用,利用数形结合是解决本题的关键.综合性较强,运算量较大.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
如果实数x,y满足
,则
的最大值为( )
|
| 4x+2y-16 |
| x-3 |
A、
| ||
| B、6 | ||
| C、7 | ||
| D、8 |
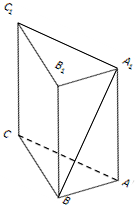 如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2