题目内容

若直线l的方程为kx-y+1-k=0（k∈R），则直线l与椭圆
x2
9
+
y2
4
=1的交点个数为
 
．
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由直线系方程求得直线恒过定点（1，1），且得到定点在椭圆内部，则答案可求．
解答： 解：由题意得直线l的方程为k（x-1）=y-1，恒过定点（1，1），
又
1
9
+
1
4
＜1，
∴点（1，1）在椭圆
x2
9
+
y2
4
=1的内部，
故所求交点个数是2个．
故答案为：2．
点评：本题考查了直线与椭圆的关系，考查了直线系方程，是基础题．
练习册系列答案
相关题目
在△ABC中，
AB
=
a
，
AC
=
b
，D是BC的中点，点E在AB上，
BE
=
1
3
BA
，则
ED
=
 
．
定义x1，x2，…，xn的“倒平均数”为
n
x1+x2+…+xn
（n∈N*），已知数列{an}前n项的“倒平均数”为
1
2n+4
．
（Ⅰ）记cn=
an
n+1
（n∈N*），试比较cn与cn+1的大小；
（Ⅱ）是否存在实数，使得当x≤λ时，f（x）=-x2+4x-
an
n+1
≤0对任意n∈N*恒成立？若存在，求出最大的实数；若不存在，说明理由．
设a＞0，且a≠1，f（x）=
1
3x+
3
．
（1）求值：f（0）+f（1），f（-1）+f（2）；
（2）由（1）的结果归纳概括对所有实数x都成立的一个等式，并加以证明；
（3）若n∈N*，求和：f（-99）+f（-98）+…+f（-1）+f（0）+f（1）+…+f（100）．
常用的统计图表有
 
，常用的抽样方法有
 
．
已知F1、F2是双曲线
x2
a2
-
y2
b2
=1的左右焦点，以F1、F2为一边的等边△PF1F2与双曲线的两交点MN恰好为等边三角形两边中点，则双曲线离心率为
 
．
化简：sin4θ-cos4θ=
 
．
已知椭圆的标准方程x2+
y2
10
=1，则椭圆的焦点坐标为（　　）
A、(±
10
，0)
B、(0，±
10
)
C、（0，±3）
D、（±3，0）
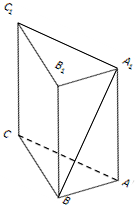如图，已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上，若AA1⊥平面A1B1C1，A1B1⊥B1C1，AA1=8，A1B1=6，A1C1=2
34
，则球O的体积为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网