题目内容
某工厂生产A和B两种产品,已知制造产品A1kg,要用煤9t,电力4kw,劳动力3个,能创造经济价值7万元;制造产品B1kg,要用煤4t,电力5kw,劳动力10个,能创造经济价值12万元,现在该工厂有煤360t,电力200kw,劳动力300个,问在这种限制条件下,应生产产品A、B各多少千克,才能使所创造的总的经济价值最高?
考点:简单线性规划的应用
专题:应用题,不等式的解法及应用
分析:由题意,设生产产品A、B各x,y千克,所创造的总的经济价值为z万元;从而得到线性约束条件及目标函数,利用线性规划求解.
解答:
解:设生产产品A、B各x,y千克,所创造的总的经济价值为z万元;
则由题意可得,
;
z=7x+12y;
作平面区域如右图;
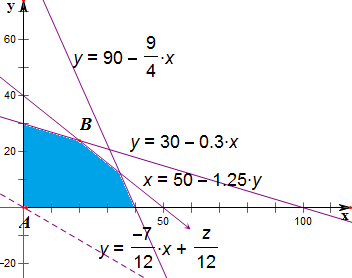
由图可知,
,解得,x=20,y=24;
即当生产A20kg,B24kg才能创造最高经济价值7×20+12×24=428(万元).
则由题意可得,
|
z=7x+12y;
作平面区域如右图;

由图可知,
|
即当生产A20kg,B24kg才能创造最高经济价值7×20+12×24=428(万元).
点评:本题考查了线性规划在实际问题中的应用,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知椭圆的标准方程x2+
=1,则椭圆的焦点坐标为( )
| y2 |
| 10 |
A、(±
| ||
B、(0,±
| ||
| C、(0,±3) | ||
| D、(±3,0) |
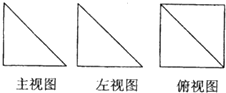 一个几何体的三视图如图所示,其中正视图和侧(左)视图是腰长为4的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧(左)视图是腰长为4的两个全等的等腰直角三角形,则该几何体的体积为( )| A、16 | ||
| B、64 | ||
C、
| ||
D、
|
如果实数x,y满足
,则
的最大值为( )
|
| 4x+2y-16 |
| x-3 |
A、
| ||
| B、6 | ||
| C、7 | ||
| D、8 |
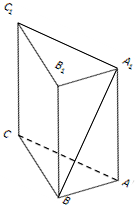 如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2