题目内容
已知f′(x)是f(x)的导函数,f(x)=ln(x+1)+m-2f′(1),m∈R,且函数f(x)的图象过点(0,-2).
(1)求函数y=f(x)的表达式;
(2)求函数g(x)=f(x)+x+
的单调区间和极值.
(1)求函数y=f(x)的表达式;
(2)求函数g(x)=f(x)+x+
| 6 |
| x+1 |
考点:利用导数研究函数的单调性,利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的概念及应用
分析:(1)由f′(x)=
,得f′(1)=
,由-2=ln1+m-2×
,解得:m=-1,从而求出函数的表达式为:y=ln(x+1)-2,
(2)由g′(x)=
+1-
=
,得函数g(x)的单调减区间为(-1,1),单调增区间为(1,+∞),从而极小值是g(1)=2+ln2,无极大值.
| 1 |
| x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由g′(x)=
| 1 |
| x+1 |
| 6 |
| (x+1)2 |
| (x+4)(x-1) |
| (x+1)2 |
解答:
解:(1)∵f′(x)=
,
∴f′(1)=
,
∵函数f(x)的图象过点(0,-2),
∴-2=ln1+m-2×
,解得:m=-1,
∴函数的表达式为:y=ln(x+1)-2,
(2)函数g(x)的定义域为(-1,+∞),
∴g′(x)=
+1-
=
,
∴当-1<x<1时,g'(x)<0;当x>1时,g'(x)>0,
∴函数g(x)的单调减区间为(-1,1),单调增区间为(1,+∞),
∴极小值是g(1)=2+ln2,无极大值.
| 1 |
| x+1 |
∴f′(1)=
| 1 |
| 2 |
∵函数f(x)的图象过点(0,-2),
∴-2=ln1+m-2×
| 1 |
| 2 |
∴函数的表达式为:y=ln(x+1)-2,
(2)函数g(x)的定义域为(-1,+∞),
∴g′(x)=
| 1 |
| x+1 |
| 6 |
| (x+1)2 |
| (x+4)(x-1) |
| (x+1)2 |
∴当-1<x<1时,g'(x)<0;当x>1时,g'(x)>0,
∴函数g(x)的单调减区间为(-1,1),单调增区间为(1,+∞),
∴极小值是g(1)=2+ln2,无极大值.
点评:本题考察了函数的单调性,函数的最值问题,导数的应用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
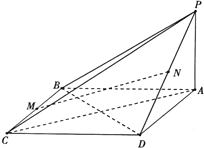 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点.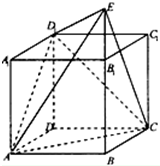 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC,设AB=2.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC,设AB=2. 如图,在底面边长为a的正方形的四棱锥P-ABCD中,已知PA⊥平面AC,且PA=a,则直线PB与平面PCD所成的角大小为
如图,在底面边长为a的正方形的四棱锥P-ABCD中,已知PA⊥平面AC,且PA=a,则直线PB与平面PCD所成的角大小为