题目内容
某学校在高一年级举行“低碳生活”知识竞赛,现有甲、乙两个班级代表队进入决赛,决赛共设20道选择题,分20轮进行,每轮1道题选择题,每道题采用抛硬币的方式来决定由哪个代表队来答题,答对得3分,答错扣1分,若规定抛出硬币正面朝上,则有甲队答题,否则由乙队答题,在第一轮比赛中,若甲队答对该题的概率为
,设甲队在第一轮比赛中所得分数为随机变量X,则随机变量X的数学期望为 分.
| 3 |
| 4 |
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:由题意知X=-1,0,3,分别求出相应的概率,由此能求出随机变量X的数学期望.
解答:
解:由题意知X=-1,0,3,
P(X=-1)=
×(1-
)=
,
P(X=0)=
,
P(X=3)=
×
=
,
∴EX=-1×
+0×
+3×
=
.
故答案为:
.
P(X=-1)=
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 8 |
P(X=0)=
| 1 |
| 2 |
P(X=3)=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
∴EX=-1×
| 1 |
| 8 |
| 1 |
| 2 |
| 3 |
| 4 |
| 17 |
| 8 |
故答案为:
| 17 |
| 8 |
点评:本题考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
设P(x,y)是函数y=
+lnx图象上的点,则x+y的最小值为( )
| 2 |
| x |
| A、3 | ||
| B、2 | ||
C、
| ||
| D、3+ln2 |
类比边长为2a的正三角形内的一点到三边的距离之和为
a,对于棱长为6a的正四面体,正确的结论是( )
| 3 |
A、正四面体内部的一点到六条棱的距离的和为2
| ||
B、正四面体内部的一点到四面的距离的和为2
| ||
C、正四面体的中心到四面的距离的和为2
| ||
D、正四面体的中心到六条棱的距离的和为9
|
若a<0、b>0,则下列不等式中正确的是( )
| A、|a|>|b| | ||||
| B、a2<b2 | ||||
C、
| ||||
D、
|
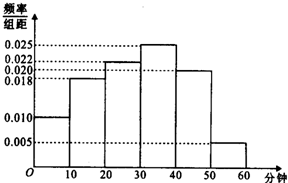 电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.右图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.右图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.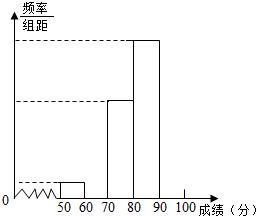 中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.