设Sn为等差数列{an}的前n项和.若S3=3.S6=24.则a9=15．题目和参考答案——青夏教育精英家教网—

题目内容

11．设S_n为等差数列{a_n}的前n项和，若S₃=3，S₆=24，则a₉=15．

分析利用等差数列的前n项和公式列出方程组，求出首项与公差，由此能求出a₉．

解答解：∵S_n为等差数列{a_n}的前n项和，若S₃=3，S₆=24，
∴$\left\{\begin{array}{l}{3{{a}_{1}+\frac{3×2}{2}d=3}^{\;}}\\{6{a}_{1}+\frac{6×5}{2}d=24}\end{array}\right.$，
解得a₁=-1，d=2，
∴a₉=-1+8×2=15．
故答案为：15．

点评本题考查等差数列的第9项的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案

2．直线a、b是异面直线，α、β是平面，若a?α，b?β，α∩β=c，则下列说法正确的是（　　）

	A．	c至少与a、b中的一条相交		B．	c至多与a、b中的一条相交
	C．	c与a、b都相交		D．	c与a、b都不相交

19．直线（1-2a）x-2y+3=0与直线3x+y+2a=0垂直，则实数a的值为（　　）

6．给出以下结论：
①有两个侧面是矩形的棱柱是直棱柱；
②有两个相邻侧面是矩形的棱柱是正棱柱；
③各侧面都是正方形的棱柱一定是正棱柱；
④一个三棱锥四个面可以都为直角三角形；
⑤长方体一条对角线与同一个顶点的三条棱所成的角为α，β，γ，则cos²α+cos²β+cos²γ=1．
其中正确的是④⑤（将正确结论的序号全填上）

16．已知函数f（x）=sin（$\frac{5π}{2}$-ωx）（ω＞0），且其图象上相邻最高点、最低点的距离为$\sqrt{4+{π}^{2}}$．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若已知sinα+f（α）=$\frac{2}{3}$，求$\frac{2sinαcosα-2si{n}^{2}α}{1+tanα}$的值．

3．下列命题为真命题的是（　　）

	A．	已知x，y∈R，则$\left\{\begin{array}{l}{x＞1}\\{y＞2}\end{array}\right.$是$\left\{\begin{array}{l}{x+y＞3}\\{xy＞2}\end{array}\right.$的充要条件
	B．	当0＜x≤2时，函数y=x-$\frac{1}{x}$无最大值
	C．	?a，b∈R，$\frac{a+b}{2}≥\sqrt{ab}$
	D．	?x∈R，sinx+cosx=$\frac{7}{5}$

20．设f（x）=1-cosx，则f′（$\frac{π}{2}$）等于（　　）

1．

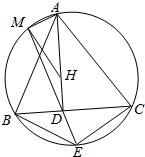如图，△ABC的垂心为H，AD⊥BC于D，点E在△ABC的外接圆上，且满足$\frac{BE}{CE}$=$\frac{AB}{AC}$，直线ED交外接圆于点M，求证：∠AMH=90°．

试题分类