题目内容

1．函数f（x）=x+lnx的零点个数是（　　）
A．3B．2C．1D．0

分析 根据一次函数的对数函数的单调性，结合增函数的性质，可判断出函数f（x）=lnx+x在（0，+∞）上为增函数，故函数f（x）至多有一个零点，进而根据f（$\frac{1}{e}$）•f（1）＜0，可得函数f（x）在区间（$\frac{1}{e}$，1）上有一个零点．

解答 解：∵y=lnx与y=x均在（0，+∞）上为增函数
故函数f（x）=lnx+x在（0，+∞）上为增函数
故函数f（x）至多有一个零点
又∵f（$\frac{1}{e}$）=$\frac{1}{e}$-1＜0，f（1）=1＞0
∴f（$\frac{1}{e}$）•f（1）＜0，
即函数f（x）在区间（$\frac{1}{e}$，1）上有一个零点
故选：C．

点评 本题考查的知识点是根的存在性及根的个数判断，熟练掌握零点存在定理是解答的关键．

练习册系列答案
相关题目
2．求证：$\frac{π}{2}$是函数f（x）=|sin（2x+$\frac{π}{8}$）|的一个周期．
12．数列{an}满足${a_{n+1}}=\frac{{2{a_n}-9}}{{{a_n}-4}}（{n∈{N^+}}）$，且a1=2．
（1）写出a2，a3，a4的值；
（2）归纳猜想数列{an}的通项公式，并用数学归纳法证明；
（3）设${b_n}=（{{a_{n+1}}-3}）（{{a_n}-3}）（{n∈{N^+}}）$，求数列{bn}的前n项和Tn．
9．已知函数f（x）=3x，x∈[-1，1]，函数g（x）=[f（x）]2-2af（x）+3．
（Ⅰ）当a=0时，求函数g（x）的值域；
（Ⅱ）若函数g（x）的最小值为h（a），求h（a）的表达式；
（Ⅲ）是否存在实数m，n同时满足下列两个条件：①m＞n＞3；②当h（a）的定义域为[n，m]时，值域为[n2，m2]？若存在，求出m，n的值；若不存在，请说明理由．
16．定义A*B、B*C、C*D、D*B分别对应下列图形，

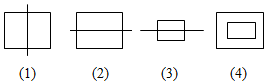
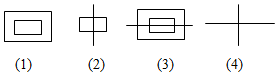
那么下面的图形中，可以表示A*D，A*C的分别是（　　）
A．（1）、（2）B．（2）、（3）C．（2）、（4）D．（1）、（4）
6．给出以下结论：
①有两个侧面是矩形的棱柱是直棱柱；
②有两个相邻侧面是矩形的棱柱是正棱柱；
③各侧面都是正方形的棱柱一定是正棱柱；
④一个三棱锥四个面可以都为直角三角形；
⑤长方体一条对角线与同一个顶点的三条棱所成的角为α，β，γ，则cos2α+cos2β+cos2γ=1．
其中正确的是④⑤（将正确结论的序号全填上）
13．已知曲线C上的点到直线x=-2的距离比它到点F（1，0）的距离大1．
（Ⅰ）求曲线C的方程；
（Ⅱ）过点F（1，0）做斜率为k的直线交曲线C于M，N两点，求证：$\frac{1}{|MF|}$+$\frac{1}{|NF|}$为定值．
10．“x≤2或x≥5”是“x2-7x+10＞0”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
11．某学校为了解三年级、六年级、九年级这三个年级学生的视力情况，拟从中抽取一定比例的学生进行调杳，则最合理的抽样方法是（　　）
A．抽签法B．系统抽样法C．分层抽样法D．随机数法

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网