题目内容
若不等式组
表示的平面区域经过四个象限，则实数λ的取值范围是（ ）
|
| A、（-∞，2） |
| B、[-1，1] |
| C、[-1，2） |
| D、（1，+∞） |
考点：简单线性规划
专题：不等式的解法及应用
分析：判断直线λx-y+2λ-2=0过定点（-2，-2），作出不等式组对应的平面区域，利用数形结合即可得到结论．
解答：
解：直线λx-y+2λ-2=0等价为λ（x+2）-y-2=0，则直线过定点（-2，-2），
作出不等式组对应的平面区域如图：
要使不等式组表示的平面区域经过四个象限，
则原点O必须在直线λx-y+2λ-2=0的下方，
即当x=0，y=0时，不等式λx-y+2λ-2＞0成立，
即2λ-2＞0，
∴解得λ＞1，
故选：D
解：直线λx-y+2λ-2=0等价为λ（x+2）-y-2=0，则直线过定点（-2，-2），作出不等式组对应的平面区域如图：
要使不等式组表示的平面区域经过四个象限，
则原点O必须在直线λx-y+2λ-2=0的下方，
即当x=0，y=0时，不等式λx-y+2λ-2＞0成立，
即2λ-2＞0，
∴解得λ＞1，
故选：D
点评：本题主要考查线性规划中的区域问题，利用数形结合时即可得到结论．
练习册系列答案
相关题目
设函数f（x）=xa+1（a∈Q）的定义域为[-b，-a]∪（a，b]，其中0＜a＜b，且f（x）在[a，b]上的最大值为6，最小值为3，则f（x）在[-b，-a]上的最大值与最小值的和是（ ）
| A、-5 | B、9 |
| C、-5或9 | D、以上不对 |
已知直线a和平面α，则能推出a∥α的是（ ）
| A、存在一条直线b，a∥b，且b∥α |
| B、存在一条直线b，a⊥b，且b⊥α |
| C、存在一个平面β，a?β，且α∥β |
| D、存在一个平面β，a∥β，且α∥β |
已知函数y=f（x）的导函数y=f′（x）的图象如图，则（ ）
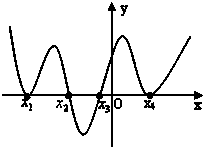
| A、函数f（x）有2个极大值点，2个极小值点 |
| B、函数f（x）有1个极大值点，1个极小值点 |
| C、函数f（x）有3个极大值点，1个极小值点 |
| D、函数f（x）有1个极大值点，3个极小值点． |
过双曲线
-
=1（a＞0，b＞0）的左焦点F（-c，0）作圆x2+y2=a2的切线，切点为E，延长FE交抛物线y2=4cx于点P，O为原点，若|FE|=|EP|，则双曲线离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
甲、乙两人下棋，两人下成和棋的概率是
，乙获胜的概率是
，则乙不输的概率是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|