题目内容

5．已知命题“?x∈R，使4x2+（a-2）x+$\frac{1}{4}$≤0”是假命题，则实数a的取值范围是（　　）
A．（-∞，0）B．[0，4]C．[4，+∞）D．（0，4）

分析 根据特称命题的真假关系即可得到结论．

解答 解：∵命题“?x∈R，使4x2+（a-2）x+$\frac{1}{4}$≤0”是假命题，
∴命题“?x∈R，使4x2+（a-2）x+$\frac{1}{4}$＞0”是真命题，
即判别式△=（a-2）2-4×4×$\frac{1}{4}$＜0，
即△=（a-2）2＜4，
则-2＜a-2＜2，即0＜a＜4，
故选：D．

点评 本题主要考查含有量词的命题的真假应用，利用一元二次不等式的性质是解决本题的关键．

练习册系列答案
相关题目
15．已知命题p：?c＞0，使方程x2-x+c=0有解，则￢p为（　　）
A．?c＞0，方程x2-x+c=0无解B．?c≤0，方程x2-x+c=0有解
C．?c＞0，使方程x2-x+c=0无解D．?c≤0，使方程x2-x+c=0有解
16．若集合A={x|x2+x-6＞0}，集合B={x|-2＜x＜4}，则A∩B等于（　　）
A．∅B．（-2，3）C．（3，4）D．（2，4）
13．若命题“?x0∈R，ax02-ax0-2≥0”是假命题，则实数a的取值范围是（-8，0]．
20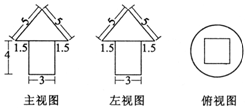．如图是一个几何体的三视图，尺寸如图所示，（单位：cm），则这个几何体的体积是（　　）
A．（10π+36）cm3B．（11π+35）cm3C．（12π+36）cm3D．（13π+34）cm3
10．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}x=3+tcosα\\ y=1+tsinα\end{array}\right.$（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴）中，曲线C的方程ρ=4cosθ．
（1）求曲线C的直角坐标系方程；
（2）若点P（3，1），设圆C与直线l交于点A，B，求|PA|+|PB|的最小值．
17．某几何体的三视图如图所示，则俯视图的面积为（　　）
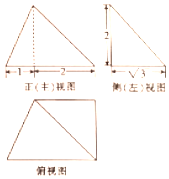
A．$5\sqrt{3}$B．$\frac{{5\sqrt{3}}}{2}$C．5D．$\frac{5}{2}$
14．空间的点M（1，0，2）与点N（-1，2，0）的距离为（　　）
A．$2\sqrt{2}$B．3C．$2\sqrt{3}$D．4
15．设数列{an}的前n项和为Sn，对任意n∈N*，函数f（x）=x2-Sncosx+2an-n在定义域内有唯一的零点．若不等式$\frac{λ}{n}$≥$\frac{n+1}{{a}_{n}+1}$对任意n∈N*恒成立，则实数λ的最小值是（　　）
A．1B．$\frac{5}{4}$C．$\frac{3}{2}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网