题目内容
14．空间的点M（1，0，2）与点N（-1，2，0）的距离为（ ）| A． | $2\sqrt{2}$ | B． | 3 | C． | $2\sqrt{3}$ | D． | 4 |
分析 直接利用空间两点间的距离公式，即可得出结论．
解答 解：∵M（1，0，2）与点N（-1，2，0），
∴|MN|=$\sqrt{（1+1）^{2}+（0-2）^{2}+（2-0）^{2}}$=2$\sqrt{3}$．
故选C．
点评 本题着重考查空间两点间的距离公式，考查学生的计算能力，属于基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
4．设集合A={-2，-1，0，1，2}，B={x|x2+2x＜0}，则A∩（∁RB）=（ ）
| A． | {1，2} | B． | {0，1，2} | C． | {-2，1，2} | D． | {-2，0，1，2} |
5．已知命题“?x∈R，使4x2+（a-2）x+$\frac{1}{4}$≤0”是假命题，则实数a的取值范围是（ ）
| A． | （-∞，0） | B． | [0，4] | C． | [4，+∞） | D． | （0，4） |
2．若tanα＜0，cosα＜0，则α的终边所有的象限为（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
阅读如图程序框图，并根据该程序框图回答以下问题：
6．
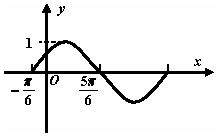已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）图象如图所示，则下列关于函数 f （x）的说法中正确的是（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）图象如图所示，则下列关于函数 f （x）的说法中正确的是（ ）| A． | 对称轴方程是x=$\frac{π}{6}$+kπ（k∈Z） | B． | 对称中心坐标是（$\frac{π}{3}$+kπ，0）（k∈Z） | ||
| C． | 在区间（-$\frac{π}{2}$，$\frac{π}{2}$）上单调递增 | D． | 在区间（-π，-$\frac{2π}{3}$）上单调递减 |