题目内容
10.在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}x=3+tcosα\\ y=1+tsinα\end{array}\right.$(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,曲线C的方程ρ=4cosθ.(1)求曲线C的直角坐标系方程;
(2)若点P(3,1),设圆C与直线l交于点A,B,求|PA|+|PB|的最小值.
分析 (1)利用互化公式可得直角坐标方程.
(2)将l的参数方程代入圆C的直角坐标方程,得t2+2(cosα-sinα)t-2=0,利用根与系数的关系、参数的几何意义即可得出.
解答 解:(1)曲线C的方程ρ=4cosθ,化为直角坐标方程:(x-2)2+y2=4;
(2)将l的参数方程代入圆C的直角坐标方程,得t2+2(cosα-sinα)t-2=0,
可设t1,t2是上述方程的两根,
所以t1+t2=-2(cosα-sinα),t1t2=-2
又直线过点(3,1),故结合t的几何意义得|PA|+|PB|=|t1-t2|=$\sqrt{12+4sin2α}≥2\sqrt{2}$,
所以PA|+|PB|的最小值为2$\sqrt{2}$.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、直线与圆相交弦长问题、一元二次方程的根与系数,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据,根据上表提供的数据,求出y关于x的线性回归方程y=0.75x+0.35,那么表中m=3.9.
| X | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
1.已知变量x、y满足约束条件$\left\{\begin{array}{l}x+y-3≥0\\ 3x-y-3≥0\\ x≤a\end{array}\right.$若$\frac{y}{x+1}$的最大值为2,则$\frac{y}{x+1}$的最小值为( )
| A. | $\frac{1}{6}$ | B. | $-\frac{3}{5}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{3}$ |
5.已知命题“?x∈R,使4x2+(a-2)x+$\frac{1}{4}$≤0”是假命题,则实数a的取值范围是( )
| A. | (-∞,0) | B. | [0,4] | C. | [4,+∞) | D. | (0,4) |
2.若tanα<0,cosα<0,则α的终边所有的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 阅读如图程序框图,并根据该程序框图回答以下问题:
阅读如图程序框图,并根据该程序框图回答以下问题: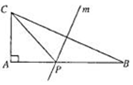 如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.
如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.