题目内容
若x∈[0,+∞),则下列不等式恒成立的有: (填上相应的序号)
①ex≤1+x+x2
②
≤1-
x+
x2
③cosx≥1-
x2
④ln(1+x)≥x-
x2.
①ex≤1+x+x2
②
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 4 |
③cosx≥1-
| 1 |
| 2 |
④ln(1+x)≥x-
| 1 |
| 8 |
考点:利用导数研究函数的单调性,不等关系与不等式
专题:函数的性质及应用,导数的概念及应用
分析:对于①,取x=3,e3>1+3+32,即可判断;
对于②,令x=1,
,计算可得结论;
对于③,构造函数h(x)=cosx-1+
x2,h′(x)=-sinx+x,h″(x)=cosx+1≥0,从而可得函数h(x)在[0,+∞)上单调增,故成立;
对于④,取x=3,计算可得结论.
对于②,令x=1,
| 1 |
| 2 |
对于③,构造函数h(x)=cosx-1+
| 1 |
| 2 |
对于④,取x=3,计算可得结论.
解答:
解:对于①,取x=3,e3>1+3+32,所以不等式不恒成立;
对于②,x=1时,左边=
,右边=0.75,不等式成立;
x=
时,左边=
,右边=
,左边大于右边,所以x∈[0,+∞),不等式不恒成立;
对于③,构造函数h(x)=cosx-1+
x2,h′(x)=-sinx+x,h″(x)=cosx+1≥0,
∴h′(x)在[0,+∞)上单调增,∴h′(x)≥h′(0)=0,
∴函数h(x)在[0,+∞)上单调增,∴h(x)≥0,∴cosx≥1-
x2,故③恒成立;
对于④,取x=3,ln(1+3)<3-
,所以不等式不恒成立;
故答案为:③.
对于②,x=1时,左边=
| 1 | ||
|
x=
| 1 |
| 2 |
| ||
| 3 |
| 13 |
| 16 |
对于③,构造函数h(x)=cosx-1+
| 1 |
| 2 |
∴h′(x)在[0,+∞)上单调增,∴h′(x)≥h′(0)=0,
∴函数h(x)在[0,+∞)上单调增,∴h(x)≥0,∴cosx≥1-
| 1 |
| 2 |
对于④,取x=3,ln(1+3)<3-
| 9 |
| 8 |
故答案为:③.
点评:本题考查大小比较,考查构造函数,考查导数知识的运用,确定函数的单调性是解题的关键.

练习册系列答案
相关题目
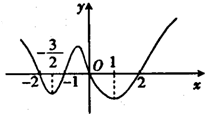 已知函数f(x)的导函数f′(x),函数y=xf′(x)的图象如图所示,则函数f(x)的增区间是( )
已知函数f(x)的导函数f′(x),函数y=xf′(x)的图象如图所示,则函数f(x)的增区间是( )| A、(-2,-1) | ||
B、(-
| ||
| C、(1,+∞) | ||
| D、(0,2) |