题目内容
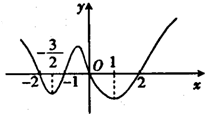 已知函数f(x)的导函数f′(x),函数y=xf′(x)的图象如图所示,则函数f(x)的增区间是( )
已知函数f(x)的导函数f′(x),函数y=xf′(x)的图象如图所示,则函数f(x)的增区间是( )| A、(-2,-1) | ||
B、(-
| ||
| C、(1,+∞) | ||
| D、(0,2) |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:根据函数y=xf′(x)的图象,求出f′(x)>0的区间,即可求出函数的单调递增区间.
解答:
解:由y=xf′(x)的图象,可知,
当-2<x<-1时,xf′(x)<0,此时f′(x)>0,此时函数单调递增,
当0<x<2时,xf′(x)<0,此时f′(x)<0,此时函数单调递减,
当x>2时,xf′(x)>0,此时f′(x)>0,此时函数单调递增,
故函数的单调递增区间为(-2,-1),(2,+∞),
故选:A.
当-2<x<-1时,xf′(x)<0,此时f′(x)>0,此时函数单调递增,
当0<x<2时,xf′(x)<0,此时f′(x)<0,此时函数单调递减,
当x>2时,xf′(x)>0,此时f′(x)>0,此时函数单调递增,
故函数的单调递增区间为(-2,-1),(2,+∞),
故选:A.
点评:本题主要考查函数单调区间的判断,根据函数图象,求出f′(x)>0的区间是解决本题的关键.

练习册系列答案
相关题目
用一个平行于棱锥底面的平面截这个棱锥,截得的棱台上、下底面面积比为1:4,截去的棱锥的高是3cm,则棱台的高是( )
| A、12cm | B、9cm |
| C、6cm | D、3cm |
已知m,n为两条不同的直线,α,β为两个不同的平面,下列四个命题中,正确的是( )
| A、若m∥α,且n∥α,则m∥n |
| B、若m,n在α上,且m∥β,n∥β,则α∥β |
| C、若α⊥β,且m在α上,则m⊥β |
| D、若α⊥β,m⊥β,m在α外,则m∥α |
方程x3-3x2+1=0的实根的个数为( )
| A、3 | B、2 | C、1 | D、0 |
记等差数列{an}的前n项和为Sn,利用倒序求和的方法得Sn=
;类似地,记等比数列{bn}的前n项积为Tn,且bn>0(n∈N*),类比等差数列求和的方法,可将Tn表示成关于首项b1,末项bn与项数n的关系式为( )
| n(a1+an) |
| 2 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
数列{an}满足a1=
,an+1=1-
,则a2014等于( )
| 1 |
| 2 |
| 1 |
| an |
A、
| ||
| B、-1 | ||
| C、2 | ||
| D、3 |
若α是钝角,则θ=kπ+α,k∈Z是( )
| A、第二象限角 |
| B、第三象限角 |
| C、第二象限角或第三象限角 |
| D、第二象限角或第四象限角 |
一条直线与一个平面垂直的条件是( )
| A、垂直于平面内的一条直线 |
| B、垂直于平面内的两条直线 |
| C、垂直于平面内的无数条直线 |
| D、垂直于平面内的两条相交直线 |