题目内容
若函数y=f(x)的定义域为(-∞,0)∪(0,+∞),对定义域内的任意两个实数x,y,都有f(xy)=f(x)+f(y),并且当x>1时,f(x)>0,且f(4)=2
(1)证明函数y=f(x)为偶函数;
(2)证明函数f(x)在(0,+∞)上为增函数;
(3)若函数g(x)=2x-2,且当a∈[1,4]时,有f(a)=g(b),求b的取值范围.
(1)证明函数y=f(x)为偶函数;
(2)证明函数f(x)在(0,+∞)上为增函数;
(3)若函数g(x)=2x-2,且当a∈[1,4]时,有f(a)=g(b),求b的取值范围.
考点:抽象函数及其应用,函数奇偶性的判断
专题:证明题,函数的性质及应用
分析:(1)运用函数的奇偶性的定义,令x=y=1得到f(1)=0,令x=y=-1得到f(-1)=0,令y=-1则f(-x)=f(x),结论成立;
(2)运用增函数的定义证明,令0<x1<x2则
>1,f(
)>0,再由条件可得到f(x2)>f(x1),
可得证;
(3)由a∈[1,4],f(x)为增函数,求出f(a)的取值范围,再解0≤2b-2≤2,即可得到b的取值范围.
(2)运用增函数的定义证明,令0<x1<x2则
| x2 |
| x1 |
| x2 |
| x1 |
可得证;
(3)由a∈[1,4],f(x)为增函数,求出f(a)的取值范围,再解0≤2b-2≤2,即可得到b的取值范围.
解答:
(1)证明:∵定义域关于原点对称,
∴令x=y=1则f(1)=2f(1)
∴f(1)=0,
令x=y=-1则f(1)=2f(-1)
∴f(-1)=0,
令y=-1则f(-x)=f(x)+f(-1)
∴f(-x)=f(x)即y=f(x)为偶函数;
(2)证明:∵当x>1时,f(x)>0,
令0<x1<x2则
>1,
f(
)>0即f(x2)+f(
)>0,
即f(x2)-f(x1)>0,
∴f(x)在(0,+∞)上为增函数;
(3)解:由g(x)=2x-2得g(b)=2b-2,
又a∈[1,4],f(x)为增函数,
∴f(1)最大即为0,f(4)最大即为2,
即0≤2b-2≤2故1≤b≤2,
∴b的取值范围是[1,2].
∴令x=y=1则f(1)=2f(1)
∴f(1)=0,
令x=y=-1则f(1)=2f(-1)
∴f(-1)=0,
令y=-1则f(-x)=f(x)+f(-1)
∴f(-x)=f(x)即y=f(x)为偶函数;
(2)证明:∵当x>1时,f(x)>0,
令0<x1<x2则
| x2 |
| x1 |
f(
| x2 |
| x1 |
| 1 |
| x1 |
即f(x2)-f(x1)>0,
∴f(x)在(0,+∞)上为增函数;
(3)解:由g(x)=2x-2得g(b)=2b-2,
又a∈[1,4],f(x)为增函数,
∴f(1)最大即为0,f(4)最大即为2,
即0≤2b-2≤2故1≤b≤2,
∴b的取值范围是[1,2].
点评:本题主要考查函数的奇偶性和单调性及应用,注意定义的运用,以及考查解决抽象函数的常用方法:赋值法,属于中档题.

练习册系列答案
相关题目
已知某等比数列共有10项,其奇数项之和为15,偶数项之和为30,则其公比为( )
| A、5 | B、4 | C、3 | D、2 |
等差数列{an},前n项和为Sn,a1>0,a2012,a2013是方程x2-(λ2+λ+1)x-(λ2+1)=0的两根,则满足Sn>0的n的最大正整数为( )
| A、4023 | B、4024 |
| C、4025 | D、4026 |
在△ABC中,sinC=2sinAcosB,则△ABC的形状为( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、不能确定 |
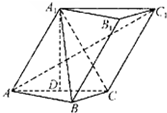 已知三棱柱ABC-A1B1C1中,∠BCA=90°,AA1=AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.
已知三棱柱ABC-A1B1C1中,∠BCA=90°,AA1=AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.