题目内容
设函数f(x)=sinx-cosx+x+1,0<x<2π,
(1)写出函数f(x)的递减区间;
(2)讨论函数f(x)的极大值或极小值,如有试写出极值.
(1)写出函数f(x)的递减区间;
(2)讨论函数f(x)的极大值或极小值,如有试写出极值.
考点:两角和与差的正弦函数,正弦函数的单调性
专题:导数的综合应用,三角函数的图像与性质
分析:(1)对函数f(x)=sinx-cosx+x+1求导,对导函数用辅助角公式变形,利用导数等于0得极值点,通过列表求出函数单调递减区间;
(2)由(1)中的表格和极值点的两侧导数的正负,求函数极大值和极小值.
(2)由(1)中的表格和极值点的两侧导数的正负,求函数极大值和极小值.
解答:
解:(1)由题意得,f′(x)=cosx+sinx+1=
sin(x+
)+1,
令f′(x)=0,得sin(x+
)=-
,
由0<x<2π得,x=π,或x=
,
当x变化时,f′(x),f(x)变化情况如下表:
由上表知f(x)的单调递减区间是(π,
);
(2)由(1)中的表格知,函数f(x)的极小值为f(
)=
,
极大值为f(π)=π+2.
| 2 |
| π |
| 4 |
令f′(x)=0,得sin(x+
| π |
| 4 |
| ||
| 2 |
由0<x<2π得,x=π,或x=
| 3π |
| 2 |
当x变化时,f′(x),f(x)变化情况如下表:
| x | (0,π) | π | (π,
|
| (
| ||||||
| f′(x) | + | 0 | - | 0 | + | ||||||
| f(x) | 单调递增 | π+2 | 单调递减 |
| 单调递增 |
| 3π |
| 2 |
(2)由(1)中的表格知,函数f(x)的极小值为f(
| 3π |
| 2 |
| 3π |
| 2 |
极大值为f(π)=π+2.
点评:本题考查利用导数研究函数的单调性与极值,利用导数为0得可能的极值点,通过列表得每个区间导数的正负判断函数的单调性,进而得出极值点.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
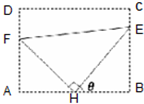 如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10
如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10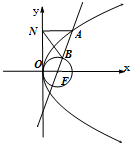 如图,抛物线C:y2=2px(p>0)的焦点为F,A为C上的点,以F为圆心,
如图,抛物线C:y2=2px(p>0)的焦点为F,A为C上的点,以F为圆心,