题目内容
若(ax2+
)6的展开式中x3项的系数为20,则a2+b2的最小值为( )
| b |
| x |
| A、1 | B、2 | C、3 | D、4 |
考点:二项式定理的应用
专题:计算题,不等式的解法及应用,二项式定理
分析:运用二项式展开式的通项公式,化简整理,再由条件得到方程,求出r=3,进而得到ab=1,再由重要不等式a2+b2≥2ab,即可得到最小值.
解答:
解:(ax2+
)6的展开式的通项公式为
Tr+1=
(ax2)6-r•(
)r=
•a6-r•br•x12-3r,
由于x3项的系数为20,则12-3r=3,
解得,r=3,
即有
•(ab)3=20,即有ab=1,
则a2+b2≥2ab=2,
当且仅当a=b,取得最小值2.
故选B.
| b |
| x |
Tr+1=
| C | r 6 |
| b |
| x |
| C | r 6 |
由于x3项的系数为20,则12-3r=3,
解得,r=3,
即有
| C | 3 6 |
则a2+b2≥2ab=2,
当且仅当a=b,取得最小值2.
故选B.
点评:本题考查二项式定理和通项公式的运用,考查重要不等式的运用:求最值,考查运算能力,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
若关于实数x的不等式x3-3x2-9x≥m对任意x∈[-2,2]恒成立,则m的取值范围是( )
| A、(-∞,5] |
| B、(-∞,-22] |
| C、(-∞,-2] |
| D、[-14,5] |
已知函数f(x)=ax3+bx+4(a,b∈R),f(lg(log210))=5,则f[lg(lg2)]=( )
| A、-3 | B、-1 | C、3 | D、4 |
某几何体的三视图(单位:cm)如图所示,则该几何体的体积为:( )
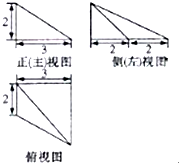

| A、2cm2 | ||
B、
| ||
C、
| ||
| D、6cm2 |
 如图,已知矩形ABCD,P为平面ABCD外一点,M、N分别为BC、PD的中点,且满足
如图,已知矩形ABCD,P为平面ABCD外一点,M、N分别为BC、PD的中点,且满足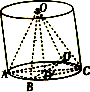 在一个圆柱中挖去一个内接正四棱锥O-ABCD(顶点是上面底面积圆的圆心O,底面是下底面的内接正方形),得到如图所示的几何体,已知圆柱底面直径为4
在一个圆柱中挖去一个内接正四棱锥O-ABCD(顶点是上面底面积圆的圆心O,底面是下底面的内接正方形),得到如图所示的几何体,已知圆柱底面直径为4