题目内容
设△ABC三边长为a、b、c,与之对应的三条高分别为Ha,Hb,Hc,若满足关系:
-
+
=6.
(1)求证S=
(3a2-b2+6c2)(S是△ABC的面积);
(2)试用b、c表示sin(A+45°),并求出角A的大小.
| 3a |
| Ha |
| b |
| Hb |
| 6c |
| Hc |
(1)求证S=
| 1 |
| 12 |
(2)试用b、c表示sin(A+45°),并求出角A的大小.
考点:余弦定理的应用
专题:综合题,解三角形
分析:(1)利用S=
aHa=
bHb=
cHc,可得Ha=
,Hb=
,Hc=
,代入
-
+
=6,即可证明结论;
(2)利用S=
(3a2-b2+6c2),结合余弦定理,三角形的面积公式,化简可得6bc(sinA+cosA)=2b2+9c2,即可用b、c表示sin(A+45°),利用基本不等式可求出角A的大小.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| a |
| 2S |
| b |
| 2S |
| c |
| 3a |
| Ha |
| b |
| Hb |
| 6c |
| Hc |
(2)利用S=
| 1 |
| 12 |
解答:
(1)证明:∵△ABC三边长为a、b、c,与之对应的三条高分别为Ha,Hb,Hc,
∴S=
aHa=
bHb=
cHc,
∴Ha=
,Hb=
,Hc=
,
∵
-
+
=6,
∴
=6,
∴S=
(3a2-b2+6c2);
(2)解:∵3a2-b2+6c2=12S,a2=b2+c2-2bccosA,
∴3b2+3c2-6bccosA-b2+6c2=12•
bcsinA
∴6bcsinA+6bccosA=2b2+9c2,
∴6bc(sinA+cosA)=2b2+9c2,
∴sin(A+45°)=
.
∵2b2+9c2≥2
=6
bc,
∴sin(A+45°)≥1,
又∵sin(A+45°)≤1,∴sin(A+45°)=1.
∴A+45°=90°,∴A=45°.
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Ha=
| 2S |
| a |
| 2S |
| b |
| 2S |
| c |
∵
| 3a |
| Ha |
| b |
| Hb |
| 6c |
| Hc |
∴
| 3a2-b2+6c2 |
| 2S |
∴S=
| 1 |
| 12 |
(2)解:∵3a2-b2+6c2=12S,a2=b2+c2-2bccosA,
∴3b2+3c2-6bccosA-b2+6c2=12•
| 1 |
| 2 |
∴6bcsinA+6bccosA=2b2+9c2,
∴6bc(sinA+cosA)=2b2+9c2,
∴sin(A+45°)=
| 2b2+9c2 | ||
6
|
∵2b2+9c2≥2
| 2b2•9c2 |
| 2 |
∴sin(A+45°)≥1,
又∵sin(A+45°)≤1,∴sin(A+45°)=1.
∴A+45°=90°,∴A=45°.
点评:本题考查三角形面积的计算,考查余弦定理,考查基本不等式,考查学生分析解决问题的能力,正确表示sin(A+45°)是关键.

练习册系列答案
相关题目
“α=
+2kπ(k∈Z)”是“cos2α=0”的( )
| π |
| 4 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不是充分条件也不是必要条件 |
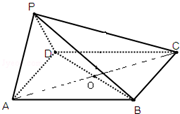 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,其对角线交点为O,侧面PAD⊥底面ABCD,且PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,其对角线交点为O,侧面PAD⊥底面ABCD,且PA=PD=