题目内容
3.不等式组$\left\{\begin{array}{l}x-y-1≥0\\ y≥-1\\ x+y-3≤0\end{array}\right.$表示的平面区域是一个三角形,则这三角形的面积为2.分析 由约束条件作出可行域,求出三角形三个顶点的坐标,得到|AB|,再由三角形面积公式得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x-y-1≥0\\ y≥-1\\ x+y-3≤0\end{array}\right.$作出可行域如图,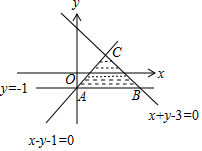
联立$\left\{\begin{array}{l}{y=-1}\\{x+y-3=0}\end{array}\right.$,解得B(4,-1),
联立$\left\{\begin{array}{l}{x-y-1=0}\\{x+y-3=0}\end{array}\right.$,解得C(2,1),又A(0,-1),
∴|AB|=4,
则${S}_{△ABC}=\frac{1}{2}×4×1=2$.
故答案为:2.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
18.过两点A(m2+2,3-m2),B(3-m-m2,-2m)的直线l的倾斜角为135°,则m的值为( )
| A. | -1或-2 | B. | -1 | C. | -2 | D. | 1 |