题目内容
已知函数f(x)=log2(x+
-2),其中常数a>0.
(1)求函数f(x)的定义域;
(2)若对任意x∈[2,+∞),恒有f(x)>0,试确定a的取值范围;
(2)记函数f(x)在[2,+∞)上的最小值为g(a),求关于a的方程g(a)=m的解(用m表示).
| a |
| x |
(1)求函数f(x)的定义域;
(2)若对任意x∈[2,+∞),恒有f(x)>0,试确定a的取值范围;
(2)记函数f(x)在[2,+∞)上的最小值为g(a),求关于a的方程g(a)=m的解(用m表示).
考点:对数函数的图像与性质,函数的最值及其几何意义,函数恒成立问题
专题:函数的性质及应用
分析:(1)得出x+
-2=
>0,分类讨论求解即可.
(2)分离参数转化为函数求解a>-x2+3x=-(x-
)2+
,得出a>2.
(3)求出函数关系式g(a)=
分段解方程即可解得a=
.
| a |
| x |
| x2-2x+a |
| x |
(2)分离参数转化为函数求解a>-x2+3x=-(x-
| 3 |
| 2 |
| 9 |
| 4 |
(3)求出函数关系式g(a)=
|
|
解答:
解:(1)x+
-2=
>0,
若a>1,定义域为{x|x>0};
若a=1,定义域为{x|x>0且x≠1};
若0<a<1,
定义域为{x|x>1+
或0<x<1-
}.
(2)x+
-2=
>0,(x≥2),
∴a>-x2+3x=-(x-
)2+
,∴a>2.
(3)g(a)=
,解得a=
.
| a |
| x |
| x2-2x+a |
| x |
若a>1,定义域为{x|x>0};
若a=1,定义域为{x|x>0且x≠1};
若0<a<1,
定义域为{x|x>1+
| 1-a |
| 1-a |
(2)x+
| a |
| x |
| x2-2x+a |
| x |
∴a>-x2+3x=-(x-
| 3 |
| 2 |
| 9 |
| 4 |
(3)g(a)=
|
,解得a=
|
点评:本题综合考查了函数的性质,运用不等式,最值问题求解,属于中档题,关键是恒等变形,构造函数.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
已知{an}是公差不为0的等差数列,{bn}是等比数列,其中a1=b1=1,a4=7,a5=b2,且存在常数a,β使得对每一个正数n都有an=1ogabn+β,则a+β=( )
| A、2 | B、4 | C、6 | D、8 |
某几何体的三视图如图所示,则该几何体的表面积( )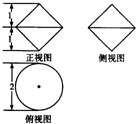

A、
| ||
B、2
| ||
C、(2
| ||
D、(2
|
 如图是一个正方体的平面展开图,则在正方体中,①CN与BE是异面直线;②平面DEM∥平面ACF;③DE⊥BM; ④AF与BM所成角为60°;⑤BN⊥平面AFC,在以上的五个结论中,正确的是
如图是一个正方体的平面展开图,则在正方体中,①CN与BE是异面直线;②平面DEM∥平面ACF;③DE⊥BM; ④AF与BM所成角为60°;⑤BN⊥平面AFC,在以上的五个结论中,正确的是