已知函数$f(x)=\left\{\begin{array}{l}x{e^x}\end{array}\right.$.若函数g-m有3个零点.则m的取值范围是．题目和参考答案——青夏教育精英家教网——

题目内容

3．已知函数$f（x）=\left\{\begin{array}{l}x{e^x}（x＜0）\\-2x（x≥0）\end{array}\right.$，若函数g（x）=f（x）-m有3个零点，则m的取值范围是（-$\frac{1}{e}$，0）．

分析由题意可得f（x）=m有3个不同实数根．画出函数f（x）的图象，通过图象即可得到所求m的范围．

解答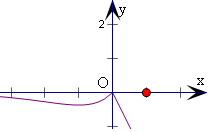解：函数g（x）=f（x）-m有3个零点，
即为f（x）=m有3个不同实数根．
当x≥0时，f（x）=-2x≤0；
当x＜0时，f（x）=xe^x，导数f′（x）=（1+x）e^x，
当-1＜x＜0时，f′（x）＞0，f（x）递增；
当x＜-1时，f′（x）＜0，f（x）递减．
可得f（x）在x＜0时由最小值，且为-$\frac{1}{e}$．
画出f（x）的图象，可得
当-$\frac{1}{e}$＜m＜0，函数f（x）和直线y=m有3个交点，
函数g（x）=f（x）-m有3个零点．
故答案为：（-$\frac{1}{e}$，0）．

点评不同考查函数零点个数问题的解法，注意运用转化思想，考查数形结合思想方法，属于中档题．

练习册系列答案

培优竞赛新方法系列答案

素养提升讲练系列答案

数学指导系列答案

导学与训练系列答案

导与学学案导学系列答案

地道中考系列答案

地理图册系列答案

第一测评系列答案

点金系列答案

点睛学案系列答案

相关题目

13．如果p是q的充分不必要条件，r是q的必要不充分条件；那么（　　）

14．将含有3n个正整数的集合M分成元素个数相等且两两没有公共元素的三个集合A、B、C，其中A={a₁，a₂，…，a_n}，B={b₁，b₂，…，b_n}，C={c₁，c₂，…，c_n}，若A、B、C中的元素满足条件：c₁＜c₂＜…＜c_n，a_k+b_k=c_k，k=1，2，…，n，则称M为“完并集合”．
（1）若M={1，x，3，4，5，6}为“完并集合”，求x的值；
（2）对于“完并集合”M={1，2，3，4，5，6，7，8，9，10，11，12}，在所有符合条件的集合C中，求元素乘积最小的集合C．

11．若双曲线上存在点P，使得P到两个焦点的距离之比为2：1，则称此双曲线存在“L点”，下列双曲线中存在“L点”的是（　　）

${x^2}-\frac{y^2}{4}=1$

${x^2}-\frac{y^2}{9}=1$

${x^2}-\frac{y^2}{15}=1$

${x^2}-\frac{y^2}{24}=1$

18．已知函数f（x）=x+$\frac{k}{|x|}$-1（x≠0），k∈R．
（1）当k=3时，试判断f（x）在（-∞，0）上的单调性，并用定义证明；
（2）若对任意x∈R，不等式f（2^x）＞0恒成立，求实数k的取值范围；
（3）当k∈R时，试讨论f（x）的零点个数．

8．已知O为原点，过双曲线$\frac{{x}^{2}}{{a}^{2}}$-y²=1（a＞0）上的点P作两条渐近线的平行线，且与两渐近线的交点分别为A，B，平行四边形OBPA的面积为2，则此双曲线的渐近线方程为（　　）

y=±$\frac{1}{4}$x

y=±$\frac{1}{3}$x

y=±$\frac{1}{2}$x

y=±$\frac{\sqrt{3}}{3}$x

15．小芳投掷一枚均匀的骰子，则它投掷得的点数为奇数的概率为（　　）

12．sin80°cos70°+sin10°sin70°=（　　）

-$\frac{\sqrt{3}}{2}$

$\frac{\sqrt{3}}{2}$

13．一个半径是R的扇形，其周长为4R，则该扇形圆心角的弧度数为（　　）

$\frac{2π}{3}$