题目内容
若
≠kx(k∈R)对于一切x∈[
,5]均成立,则有( )
| x-1 |
| 10 |
| 9 |
A、
| ||||
B、
| ||||
C、k<
| ||||
D、k<
|
考点:函数恒成立问题
专题:函数的性质及应用
分析:由已知条件推导出k≠
对一切[
,
]均成立,由此能求出结果.
| ||
| x |
| 3 |
| 10 |
| 2 |
| 5 |
解答:
解:∵
≠kx(k∈R)对于一切x∈[
,5]均成立,
∴k≠
对一切[
,
]均成立,
∴k<
,或k>
.
故选:C.
| x-1 |
| 10 |
| 9 |
∴k≠
| ||
| x |
| 3 |
| 10 |
| 2 |
| 5 |
∴k<
| 3 |
| 10 |
| 2 |
| 5 |
故选:C.
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
某人射击10次击中目标3次,则其中恰有两次连续命中目标的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数y=cos2x+cosx,则其最小值为( )
| A、-2 | ||
B、-
| ||
| C、2 | ||
| D、0 |
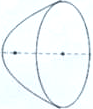 汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线的焦点出,已知灯口直径是26厘米,灯深11厘米,那灯泡与反射镜的顶点距离为
汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线的焦点出,已知灯口直径是26厘米,灯深11厘米,那灯泡与反射镜的顶点距离为