题目内容
关于x的不等式E:ax2+ax-2≤0,其中a∈R.
(Ⅰ)若a=1时,求不等式E的解集;
(Ⅱ)若不等式E在R上恒成立,求实数a的取值范围.
(Ⅰ)若a=1时,求不等式E的解集;
(Ⅱ)若不等式E在R上恒成立,求实数a的取值范围.
考点:一元二次不等式的解法
专题:计算题,不等式的解法及应用
分析:(Ⅰ)当a=1时,不等式为x2+x-2≤0,求得方程根并借助图象可求;
(Ⅱ)分a=0,a≠0两种情况讨论,a=0易判断;a≠0时,可得
,解出a;两种情况求并集;
(Ⅱ)分a=0,a≠0两种情况讨论,a=0易判断;a≠0时,可得
|
解答:
解:(Ⅰ)当a=1时,不等式为x2+x-2≤0,
∴(x+2)(x-1)≤0,
解得-2≤x≤1,
∴原不等式的解集为[-2,1];
(Ⅱ)①当a=0时,不等式化为-2≤0,
∴a=0满足题意;
②当a≠0时,则
,解得
,
∴-8≤a<0;
综合①②得-8≤a≤0.
∴(x+2)(x-1)≤0,
解得-2≤x≤1,
∴原不等式的解集为[-2,1];
(Ⅱ)①当a=0时,不等式化为-2≤0,
∴a=0满足题意;
②当a≠0时,则
|
|
∴-8≤a<0;
综合①②得-8≤a≤0.
点评:该题考查一元二次不等式的求法,考查数形结合思想,属基础题.

练习册系列答案
相关题目
“x<2”是“x2<4”的( )
| A、必要不充分条件 |
| B、充要条件 |
| C、充分不必要条件 |
| D、既不充分又非必要条件 |
已知函数f(x)=xlnx,则其在点(e,f(e))处的切线方程是( )
| A、y=2x-e | B、y=e |
| C、y=x-e | D、y=x+e |
二进制数110011(2)转化为十进制数为( )
| A、51 | B、50 | C、49 | D、19 |
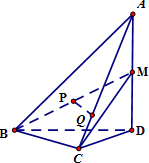 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.