题目内容
二进制数110011（2）转化为十进制数为（ ）
| A、51 | B、50 | C、49 | D、19 |
考点：整除的定义
专题：算法和程序框图
分析：利用二进制数转化为十进制数的方法即可得出．
解答：
解：二进制数110011（2）=1×25+1×24+0×23+0×22+1×21+1×20=51．
故选：A．
故选：A．
点评：本题考查了二进制数转化为十进制数的方法，属于基础题．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知集合A={0，1，2}，B={x|1＜x＜4}，则A∩B=（ ）
| A、{0} | B、{1} |
| C、{2} | D、{1，2} |
已知（1-2x）2014=a0+a1x+a2x2+…+a2014x2014，则a0+a1+a2+…+a2014=（ ）
| A、22014 |
| B、32013 |
| C、1 |
| D、-1 |
函数y=2sin2x的图象的一条对称轴方程是（ ）
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
圆内接四边形ABCD中，∠A，∠B，∠C的度数的比是3：4：6，则∠D=（ ）
| A、60° | B、80° |
| C、120° | D、100° |
若存在x∈[-2，3]，使不等式2x-x2≥a成立，则实数a的取值范围是（ ）
| A、（-∞，1] |
| B、（-∞，-8] |
| C、[1，+∞） |
| D、[-8，+∞） |
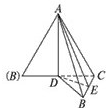如图，等边△ABC的边长为1，BC边上的高为AD，若沿AD折成直二面角，求二面角A-BC-D的正切值．