题目内容
已知R是实数集,集合M={x|
<1},N={y|y=x+
},则N∩(∁RM)=( )
| 3 |
| x |
| x-2 |
| A、[0,2] |
| B、[2,+∞) |
| C、(-∞,2] |
| D、[2,3] |
考点:交、并、补集的混合运算
专题:集合
分析:求解分式不等式化简M,求解函数的值域化简N,然后利用补集与交集概念求解.
解答:
解:由
<1,得
-1<0,即
<0,解得x<0或x>3.
∴M=(-∞,0)∪(3,+∞).
则∁RM=[0,3],
由y=x+
,令
=t(t≥0),
得x=t2+2,
∴y=t2+t+2=(t+
)2+
≥2.
∴N={y|y=x+
}=[2,+∞),
∴N∩(∁RM)=[2,3].
故选:D.
| 3 |
| x |
| 3 |
| x |
| 3-x |
| x |
∴M=(-∞,0)∪(3,+∞).
则∁RM=[0,3],
由y=x+
| x-2 |
| x-2 |
得x=t2+2,
∴y=t2+t+2=(t+
| 1 |
| 2 |
| 7 |
| 4 |
∴N={y|y=x+
| x-2 |
∴N∩(∁RM)=[2,3].
故选:D.
点评:本题考查了交集与补集的混合运算,考查了函数值域的求法,是中档题.

练习册系列答案
相关题目
下列各式错误的是( )
| A、tan138°<tan143° | ||||
B、sin(-
| ||||
| C、lg1.6>lg1.4 | ||||
| D、0.75-0.1<0.750.1 |
在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若acosB+bcosA=csinC,S=
(b2+c2-a2),则∠B=( )
| 1 |
| 4 |
| A、90° | B、60° |
| C、45° | D、30° |
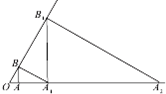 如图,在△OAB中,OA⊥AB,OB=1,OA=
如图,在△OAB中,OA⊥AB,OB=1,OA=