Question

求y=

sinx+1

cosx+2

的值域（用万能公式解）

Answer 1

考点：三角函数的最值

专题：函数的性质及应用,三角函数的求值

分析：方法一：利用万能公式，可将y=

sinx+1

cosx+2

的解析式化为y=

tan2 x 2 +2tan  x 2 +1

3+tan2 x 2

的形式，t=tan

x

2

，利用判别式法，可得函数的值域．
方法二：根据

sinx+1

cosx+2

的几何意义，画出图象，数形结合，可得函数值域．

解答： 解：∵y=

sinx+1

cosx+2

=

2tan x 2 1+tan2 x 2 +1

1-tan2 x 2 1+tan2 x 2 +2

=

tan2 x 2 +2tan x 2 +1 1+tan2 x 2

tan2 x 2 +3 1+tan2 x 2

=

tan2 x 2 +2tan  x 2 +1

3+tan2 x 2

，
令t=tan

x

2

，
则y=

t2+2t+1

3+t2

，即（y-1）t²-2t+3y-1=0，
当y=1时，方程有解；
当y≠1时，若方程有解，则△=4-4（y-1）（3y-1）≥0，
解得：y∈（0，

4

3

]，
综上：y∈[0，

4

3

]，
故y=

sinx+1

cosx+2

的值域为[0，

4

3

]．
方法二：y=

sinx+1

cosx+2

表示单位圆上一点（cosx，sinx）与（-2，-1）点连线的斜率，
如下图所示：

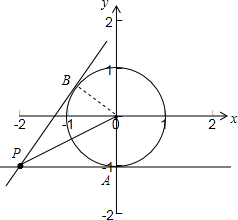
由图可知：函数y=

sinx+1

cosx+2

的值域为[k_PA，k_PB]，
∵k_PA=0，k_P0=

1

2

，k_PB=

2kPO

1-kPO2

=

4

3

，
∴y=

sinx+1

cosx+2

的值域为[0，

4

3

]．

点评：本题考查的知识点是函数的值域，万能公式，难度中档．