题目内容
椭圆的长轴为6,短轴为4,则椭圆的标准方程是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、以上都不是 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知条件,分焦点在x轴和焦点在y轴两种情况分类讨论,由此能求出椭圆的标准方程.
解答:
解:∵椭圆的长轴为6,短轴为4,
∴a=3,b=2,
∴当椭圆的焦点在x轴时,椭圆的标准方程为
+
=1;
当椭圆的焦点在y轴时,椭圆的标准方程为
+
=1.
故选:C.
∴a=3,b=2,
∴当椭圆的焦点在x轴时,椭圆的标准方程为
| x2 |
| 9 |
| y2 |
| 4 |
当椭圆的焦点在y轴时,椭圆的标准方程为
| x2 |
| 4 |
| y2 |
| 9 |
故选:C.
点评:本题考查椭圆的标准方程的求法,是基础题,解题时要认真审题,注意椭圆的简单性质的灵活运用.

练习册系列答案
相关题目
将函数y=
sinx+
cosx(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| 1 |
| 4 |
| ||
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若tan(α+β)=3,tan(α-β)=2,那么角α不可能是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
将4名学生分配到甲、乙、丙3个实验室准备实验,每个实验室至少分配1名学生的不同分配方案共有( )
| A、12种 | B、24种 |
| C、36种 | D、48种 |
已知复数z=
,则z的虚部是( )
| i3 |
| 2i+1 |
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
已知p:xy=0,q:x=0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
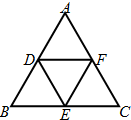 如图,已知D,E,F是正△ABC三边的中点,由A,B,C,D,E,F六点中的两点构成的向量中与
如图,已知D,E,F是正△ABC三边的中点,由A,B,C,D,E,F六点中的两点构成的向量中与