题目内容
已知函数f(x)对任意的a、b∈R都有f(a+b)=f(a)+f(b)-1,且当x>0时,f(x)>1.求证:函数F(x)=f(x)-1为奇函数.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:由题意令a=b=0,代入f(a+b)=f(a)+f(b)-1,求出f(0)的值,令a=x,b=-x,求得f(-x)=-f(x)+2,再根据奇函数的定义判断即可.
解答:
证明:∵f(a+b)=f(a)+f(b)-1,
令a=b=0,
则f(0+0)=f(0)+f(0)-1,
∴f(0)=1,
令a=x,b=-x,
则f(x-x)=f(x)+f(-x)-1,
∴f(-x)=-f(x)+2,
∵F(x)=f(x)-1
∴F(-x)=f(-x)-1=-f(x)-1=-f(x)+2=-f(x)+1=-[f(x)-1]=-F(x),
∴函数F(x)=f(x)-1为奇函数.
令a=b=0,
则f(0+0)=f(0)+f(0)-1,
∴f(0)=1,
令a=x,b=-x,
则f(x-x)=f(x)+f(-x)-1,
∴f(-x)=-f(x)+2,
∵F(x)=f(x)-1
∴F(-x)=f(-x)-1=-f(x)-1=-f(x)+2=-f(x)+1=-[f(x)-1]=-F(x),
∴函数F(x)=f(x)-1为奇函数.
点评:本题考查了抽象函数的奇偶性的证明以及求值,主要利用赋值法,即根据结论给变量适当的值,代入恒成立的方程化简即可.

练习册系列答案
相关题目
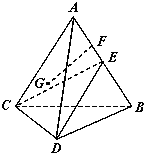 如图,在四面体ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,在四面体ABCD中,BC=AC,AD=BD,E是AB的中点. 某同学将一块底边长为5的等腰直角三角板按如图所示的方式放置在平面直角坐标系上,其中∠OMN=
某同学将一块底边长为5的等腰直角三角板按如图所示的方式放置在平面直角坐标系上,其中∠OMN= 如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.