题目内容
10.设函数f(x)=lnx+$\frac{a}{x}$+x(Ⅰ)在f(x)=lnx+$\frac{a}{x}$+x(0<x≤2)图象上任意一点P(x0,y0)处切线的斜率k≤$\frac{1}{2}$恒成立,求实数a的取值范围;
(Ⅱ)不等式f(x)≥a+1,对x∈[1,+∞)恒成立,求实数a的取值范围.
分析 (Ⅰ)求出函数的导数,问题转化为a≥${({{\frac{1}{2}x}_{0}}^{2}{+x}_{0})}_{max}$,x0∈(0,2],根据二次函数的性质求出a的范围即可;
(Ⅱ)求出函数f(x) 的导数,令g(x)=x2+x-a,(x≥1),通过讨论a的范围,求出函数的单调区间,结合函数的单调性求出a的范围即可.
解答 解:(Ⅰ)依题意,知f(x)的定义域为(0,+∞),
f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$+1,x∈(0,2],
则有k=f′(x0)=$\frac{{{x}_{0}}^{2}{+x}_{0}-a}{{{x}_{0}}^{2}}$≤$\frac{1}{2}$,在x0∈(0,2]上恒成立,
所以a≥${({{\frac{1}{2}x}_{0}}^{2}{+x}_{0})}_{max}$,x0∈(0,2],
当x0=2时,$\frac{1}{2}$${{x}_{0}}^{2}$+x0取得最大值4,所以a≥4;
(Ⅱ)由不等式f(x)≥a+1,对x∈[1,+∞)恒成立,
f′(x)=$\frac{{x}^{2}+x-a}{{x}^{2}}$,令g(x)=x2+x-a,(x≥1),
则g(x)是x∈[1,+∞)上的增函数,即g(x)≥2-a,
①当a≤2时,g(x)≥0,所以f′(x)≥0,因此f(x)是x∈[1,+∞)上的增函数,
则f(x)≥f(1)=0,因此a≤2时,不等式成立;
②当a>2时,即对x∈[1,+∞),f′(x)=0时,g(x)=0,
求得x1=$\frac{-1+\sqrt{1+4a}}{2}$,(由于x≥1,所以舍去x2=-1-$\frac{-1-\sqrt{1+4a}}{2}$)
当x∈[1,$\frac{-1+\sqrt{1+4a}}{2}$)时,f′(x)<0,则f(x)是x∈[1,$\frac{-1+\sqrt{1+4a}}{2}$)上的减函数,
当x∈$\frac{-1+\sqrt{1+4a}}{2}$,+∞)时,f′(x)>0,
则f(x)是x∈($\frac{-1+\sqrt{1+4a}}{2}$,+∞)上的增函数,
所以当x∈(1,$\frac{-1+\sqrt{1+4a}}{2}$)时,f(x)<f(1)=0,
因此a>2时,不等式不成立;
综合上述,所求范围是a≤2.
点评 本题考查了函数的单调性问题,考查导数的应用以及函数恒成立问题,是一道中档题.

 口算题天天练系列答案
口算题天天练系列答案| 实验操作 | |||||
| 不合格 | 合格 | 良好 | 优秀 | ||
| 体 能 测 试 | 不合格 | 0 | 0 | 1 | 1 |
| 合格 | 0 | 2 | 1 | b | |
| 良好 | 1 | a | 2 | 4 | |
| 优秀 | 1 | 2 | 3 | 6 | |
(Ⅰ)试确定a、b的值;
(Ⅱ)从30人中任意抽取3人,设实验操作考试和体能测试成绩都是良好或优秀的学生人数为ξ,求随机变量ξ的分布列及数学期望Eξ.
 如图,某几何体的三视图中,正视图和侧视图都是半径为$\sqrt{3}$的半圆和相同的正三角形,其中三角形的上顶点是半圆的中点,底边在直径上,则它的表面积是( )
如图,某几何体的三视图中,正视图和侧视图都是半径为$\sqrt{3}$的半圆和相同的正三角形,其中三角形的上顶点是半圆的中点,底边在直径上,则它的表面积是( )| A. | 6π | B. | 8π | C. | 10π | D. | 11π |
| A. | 3 | B. | -3 | C. | -log36 | D. | -log38 |
| A. | 是奇函数,不是偶函数 | B. | 是偶函数,不是奇函数 | ||
| C. | 既是奇函数数,又是偶函数 | D. | 既不是奇函数,也不是偶函数 |
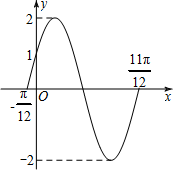 若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分图象如图所示.
若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分图象如图所示.