题目内容
5．
如图，某几何体的三视图中，正视图和侧视图都是半径为$\sqrt{3}$的半圆和相同的正三角形，其中三角形的上顶点是半圆的中点，底边在直径上，则它的表面积是（ ）| A． | 6π | B． | 8π | C． | 10π | D． | 11π |
分析 由已知中的三视图，可得该几何体是一个半球挖去一个圆锥所得的组合体，进而可得几何体的表面积．
解答 解：由已知中的三视图，可得该几何体是一个半球挖去一个圆锥所得的组合体，
由正视图和侧视图都是半径为$\sqrt{3}$的半圆和相同的正三角形，
故半球的半径为$\sqrt{3}$，
圆锥的底面半径为1，母线长为2，
故组合体的表面积S=$\frac{1}{2}×4π•{\sqrt{3}}^{2}$+（$π•{\sqrt{3}}^{2}$-π•12）+π•1•2=10π，
故选：C
点评 本题考查的知识点是圆锥的体积和表面积，球的体积和表面积，难度中档．
练习册系列答案
相关题目
13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F（c，0），圆M：（x-a）2+y2=c2，双曲线以椭圆C的焦点为顶点，顶点为焦点，若双曲线的两条渐近线都与圆M相切，则椭圆C的离心率为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{1}{2}$ |
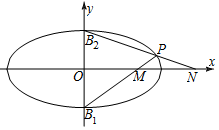椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的短轴两端点为B1（0，-1）、B2（0，1），离心率e=$\frac{\sqrt{3}}{2}$，点P是椭圆C上不在坐标轴上的任意一点，直线B1P和B2P分别与x轴相交于M，N两点，