题目内容
解关于x的不等式:
<a(a>0).
| 1-2a |
| x-2 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:转化为整式不等式,结合一元二次方程和不等式的关系分类讨论可得.
解答:
解:原不等式
<a可化为
-a<0,
整理可得
>0,即(x-2)(ax-1)>0,
当a=
时,不等式化为(x-2)2>0,只需x≠2即可,此时解集为{x|x≠2};
当0<a<
时,可得对应方程两根为2和
且2<
,可得解集为{x|x<2,或x>
};
当a>
时,可得对应方程两根为2和
且2>
,可得解集为{x|x<
,或x>2}
| 1-2a |
| x-2 |
| 1-2a |
| x-2 |
整理可得
| ax-1 |
| x-2 |
当a=
| 1 |
| 2 |
当0<a<
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
当a>
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
点评:本题考查分式不等式的解法,涉及分类讨论的思想,属中档题.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F.
如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F. 如图所示,等腰△ABC的底边AB=6
如图所示,等腰△ABC的底边AB=6
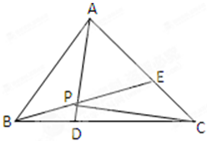 如图,在正△ABC中,点D、E分别在边BC,AC上,且BD=
如图,在正△ABC中,点D、E分别在边BC,AC上,且BD=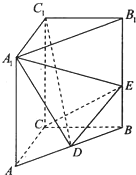 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=3,AC=BC=2,D为AB中点,E为BB1上一点,且
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=3,AC=BC=2,D为AB中点,E为BB1上一点,且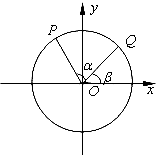 如图,以x轴负半轴为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(-
如图,以x轴负半轴为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(- 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=