题目内容
下列函数中，既是偶函数又在（0，+∞）单调递增的函数是（ ）
| A、y=x3 | ||
| B、y=|x|+1 | ||
| C、y=-x2+1 | ||
D、y=
|
考点：函数奇偶性的判断,函数单调性的判断与证明
专题：函数的性质及应用
分析：对于四个选项，首先从定义域判断是否关于原点对称，然后再利用定义判断f（-x）与f（x）的关系．
解答：
解：对于选项A是奇函数；
对于选项B，定义域是R，并且f（-x）=|-x|+1=|x|+1=f（x），是偶函数；并且在（0，+∞）单调递增的函数；
对于选项C，是偶函数，但是在（0，+∞）是单调递减的函数；
对于选项D，定义域是[0，+∞），关于原点不对称，是非奇非偶的函数．
故选：B
对于选项B，定义域是R，并且f（-x）=|-x|+1=|x|+1=f（x），是偶函数；并且在（0，+∞）单调递增的函数；
对于选项C，是偶函数，但是在（0，+∞）是单调递减的函数；
对于选项D，定义域是[0，+∞），关于原点不对称，是非奇非偶的函数．
故选：B
点评：本题考查了函数奇偶性的判定；①判断函数的定义域是否关于原点对称；②如果不对称是非奇非偶的函数；如果对称，再利用定义判断f（-x）与f（x）的关系．
练习册系列答案
相关题目
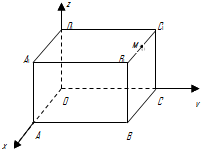如图所示的空间直角坐标系O-xyz下，长方体OABC-D1A1B1C1中，|OA|=3，|OC|=4，|OD1|=2，则B1C1的中点M的坐标是（ ）A、（
| ||
| B、（3，2，2） | ||
| C、（3，4，1） | ||
D、（
|
已知f（x）=2+log3x，x∈[
，9]，则f（x）的最小值为（ ）
| 1 |
| 81 |
| A、-2 | B、-3 | C、-4 | D、0 |
数列{an}的前n项和Sn与通项公式an满足关系式Sn=nan+2n2-2n（n∈N*），则a100-a10=（ ）
| A、-90 | B、-180 |
| C、-360 | D、-400 |
已知向量
=（1，1），
=（2，x），若
+
∥4
-2
，则实数x的值是（ ）
| a |
| b |
| a |
| b |
| b |
| a |
| A、-2 | B、0 | C、1 | D、2 |
半径为3cm，中心角为
的弧长为（ ）
| 2π |
| 3 |
A、
| ||
| B、πcm | ||
C、
| ||
| D、2πcm |
△ABC的面积是S，点P是△ABC的边AB上的一点，则△PBC的面积小于
的概率是（ ）
| S |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
| ∫ |
-
|
| A、0 | ||
| B、2 | ||
C、
| ||
D、
|
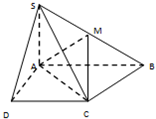如图已知四棱锥S-ABCD的底面是直角梯形，AB∥DC，∠DAB=90°，SA⊥底面ABCD，且SA=AD=DC=