题目内容
| ∫ |
-
|
| A、0 | ||
| B、2 | ||
C、
| ||
D、
|
考点：定积分
专题：计算题,导数的综合应用
分析：求出被积函数的原函数，分别代入积分上限和积分下限后作差得答案．
解答：
解：
（x3+sinx）dx=(
x4-cosx)
=
×(
)4-cos
-
×(-
)4+cos(-
)=0．
故选：A．
| ∫ |
-
|
| 1 |
| 4 |
| | |
-
|
=
| 1 |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 4 |
| π |
| 2 |
| π |
| 2 |
故选：A．
点评：本题考查了定积分，关键是求出被积函数的原函数，是基础题．
练习册系列答案
相关题目
已知全集U=R，A={x|-1＜x≤1}，B={x|2x2-1＞0}，则A∩∁UB等于（ ）
A、[
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
下列函数中，既是偶函数又在（0，+∞）单调递增的函数是（ ）
| A、y=x3 | ||
| B、y=|x|+1 | ||
| C、y=-x2+1 | ||
D、y=
|
已知命题p：
＜1，命题q：
≤1，则p是q的（ ）
| x+1 |
| 2x |
| x-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在直角坐标系xOy中，圆C的参数方程
（φ为参数）．以O为极点，x轴的非负半轴为极轴建立极坐标系，则圆C的极坐标方程是（ ）
|
| A、ρ=2cosθ |
| B、ρ=2sinθ |
| C、ρ=cosθ |
| D、ρ=sinθ |
已知单位向量
，
的夹角为
，则|
-4
|等于（ ）
| a |
| b |
| π |
| 3 |
| a |
| b |
| A、13 | ||
| B、11 | ||
C、
| ||
D、
|
已知函数sgn（x）=
，则sgn（sgn（a2-a+1））的值是（ ）
|
| A、a2-a+1 |
| B、1 |
| C、0 |
| D、-1 |
设A（3，2，1），B（1，0，5），C（0，0，1），则AB的中点M到点C的距离为（ ）
| A、1 | B、2 | C、3 | D、4 |
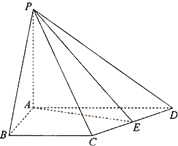如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90°，E是D的中点．证明：CD⊥平面PAE．