题目内容
9.已知对数函数f(x)图象经过点(8,3)(I)求函数f(x)的解析式;
(II)若f(x)>1,求x的范围.
分析 (Ⅰ)直接根据函数图象过点(8,3)求出对数的底,进而得出函数的解析式;(Ⅱ)解不等式求出x的范围即可.
解答 解:(Ⅰ)因为函数y=logax的图象经过点(8,3),
所以,3=loga8,解得,a=2,
因此,函数的解析式为f(x)=log2x;
(Ⅱ)由(Ⅰ)可知,f(x)=log2x,
f(x)>1即${log}_{2}^{x}$>1=${log}_{2}^{2}$,
解得:x>2.
点评 本题主要考查了对数函数的图象与性质,以及运用对数的运算性质求不等式的解,本题属于基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
20.下列计算正确的是( )
| A. | $\sqrt{{{({m-n})}^2}}=m-n$ | B. | log23×log25=log215 | ||
| C. | 210-29=29 | D. | ${({-\frac{125}{27}})^{\frac{2}{3}}}=-\frac{25}{9}$ |
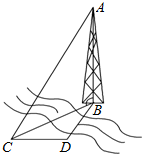 如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.
如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.