题目内容
1.作出下列函数的图象:(1)y=log2(x-1);
(2)y=|log2(x-1)|.
分析 (1)由对数函数的图象特征作函数y=log2(x-1)的图象即可;(2)根据对数函数的性质将函数f(x)表示为分段函数形式,进行作图即可.
解答 解:(1)作函数y=log2(x-1)的图象如下,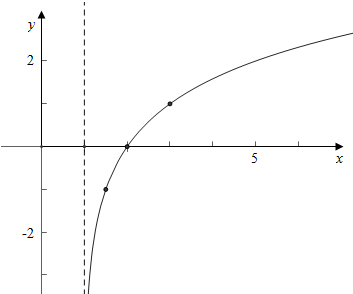 ,
,
(2)解:由log2(x-1)>0得x-1>1,即x>2,
由log2(x-1)≤0得0<x-1≤1,即1<x≤2,
即f(x)=|log2(x-1)|=$\left\{\begin{array}{l}{{log}_{2}^{(x-1)},x>2}\\{{-log}_{2}^{(x-1)},1<x≤2}\end{array}\right.$,
则对应的图象为: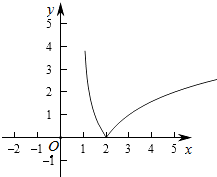
点评 本题主要考查函数图象作图,结合对数函数的性质,利用定义法是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设Sn为等比数列{an}的前n项和,且8a3+a6=0,则$\frac{S_4}{S_2}$=( )
| A. | -11 | B. | -8 | C. | 5 | D. | 11 |
6.△ABC是边长为1的正三角形,PA⊥平面ABC,且PA=$\frac{\sqrt{6}}{4}$,点A关于平面PBC的对称点为A′,则异面直线A′C与AB所成角等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
10.已知函数f(x)=x3-bx2-4,x∈R,则下列命题正确的是( )
| A. | 当b>0时,?x0<0,使得f(x0)=0 | |
| B. | 当b<0时,?x<0,都有f(x)<0 | |
| C. | f(x)有三个零点的充要条件是b<-3 | |
| D. | f(x)在区间(0.+∞)上有最小值的充要条件是b<0 |
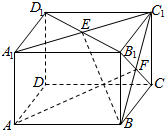 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.