题目内容
20.下列计算正确的是( )| A. | $\sqrt{{{({m-n})}^2}}=m-n$ | B. | log23×log25=log215 | ||
| C. | 210-29=29 | D. | ${({-\frac{125}{27}})^{\frac{2}{3}}}=-\frac{25}{9}$ |
分析 利用指数幂与对数的运算性质即可判断出正误.
解答 解:A.m<n时不成立,不正确;
B.log23×log25=$\frac{lg3}{lg2}•\frac{lg5}{lg2}$≠log215,不正确.
C.210-29=2•29-29=29
D.$(-\frac{125}{27})^{\frac{2}{3}}$=$(\frac{5}{3})^{3×\frac{2}{3}}$=$\frac{25}{9}$,因此不正确.
故选:C.
点评 本题考查了指数幂与对数的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
10.关于x的方程x2+x+q=0(q∈[0,1])有实根的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
12.设Sn为等比数列{an}的前n项和,且8a3+a6=0,则$\frac{S_4}{S_2}$=( )
| A. | -11 | B. | -8 | C. | 5 | D. | 11 |
10.已知函数f(x)=x3-bx2-4,x∈R,则下列命题正确的是( )
| A. | 当b>0时,?x0<0,使得f(x0)=0 | |
| B. | 当b<0时,?x<0,都有f(x)<0 | |
| C. | f(x)有三个零点的充要条件是b<-3 | |
| D. | f(x)在区间(0.+∞)上有最小值的充要条件是b<0 |
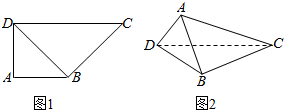 如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.
如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.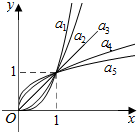 如图是幂函数$y={x^{α_i}}$(αi>0,i=1,2,3,4,5)在第一象限内的图象,其中α1=3,α2=2,α3=1,${α_4}=\frac{1}{2}$,${α_5}=\frac{1}{3}$,已知它们具有性质:
如图是幂函数$y={x^{α_i}}$(αi>0,i=1,2,3,4,5)在第一象限内的图象,其中α1=3,α2=2,α3=1,${α_4}=\frac{1}{2}$,${α_5}=\frac{1}{3}$,已知它们具有性质: