题目内容
4.已知数列{an}的通项an=n2-11n+10,则an的最小值是-20,Sn的最小值是-120.分析 an=n2-11n+10=$(n-\frac{11}{2})^{2}$-$\frac{81}{4}$,利用二次函数的单调性可得当n=5或6时,an取得最小值.由an=n2-11n+10≥0,解得n≥10或n=1.当n=9或10时,Sn取得最小值,可得Sn=(12+22+…+n2)-11(1+2+…+n)+10n=$\frac{n(n+1)(2n+1)}{6}$-$\frac{11n(n+1)}{2}$+10n.即可得出.
解答 解:an=n2-11n+10=$(n-\frac{11}{2})^{2}$-$\frac{81}{4}$,
∴当n=5或6时,an取得最小值-20.
由an=n2-11n+10≥0,解得n≥10或n=1.
∴当n=9或10时,Sn取得最小值,
Sn=(12+22+…+n2)-11(1+2+…+n)+10n
=$\frac{n(n+1)(2n+1)}{6}$-$\frac{11n(n+1)}{2}$+10n.
S9=S10=$\frac{9×10×19}{6}$-$\frac{11×9×10}{2}$+10×9
=-120.
故答案分别为:-20;-120.
点评 本题考查了二次函数的单调性、等差数列的前n项和公式、(12+22+…+n2)=$\frac{n(n+1)(2n+1)}{6}$,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
12.设Sn为等比数列{an}的前n项和,且8a3+a6=0,则$\frac{S_4}{S_2}$=( )
| A. | -11 | B. | -8 | C. | 5 | D. | 11 |
19.在△ABC中,a、b、c分别为角A、B、C所对的边,若B=60°,b2=ac,则△ABC的形状是( )
| A. | 直角三角形 | B. | 钝角三角形 | ||
| C. | 等腰非等边三角形 | D. | 等边三角形 |
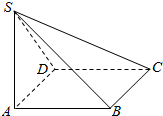 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.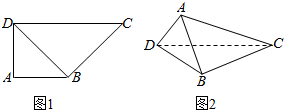 如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.
如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.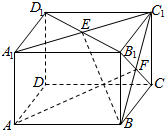 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.