题目内容
18.①不等式|2x-1|-|x+3|≤1的解集为[-1,5];②不等式|x+1|+|x-1|<5的解集为{x|x<-2.5,或x>2.5}.
分析 ①把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
②由条件利用绝对值的意义求得不等式的解集.
解答 解:①由不等式|2x-1|-|x+3|≤1,可得 $\left\{\begin{array}{l}{x<-3}\\{1-2x-(-x-3)≤1}\end{array}\right.$①,或$\left\{\begin{array}{l}{-3≤x≤\frac{1}{2}}\\{1-2x-(x+3)≤1}\end{array}\right.$②,
或$\left\{\begin{array}{l}{x>\frac{1}{2}}\\{2x-1-(x+3)≤1}\end{array}\right.$ ③.
解①求得x∈∅,解②求得-1≤x≤$\frac{1}{2}$,解③求得$\frac{1}{2}$<x≤5,
故原不等式的解集为[-1,5],
故答案为:[-1,5].
②|x+1|+|x-1|表示数轴上的x对应点到-1、1对应点的距离之和,
而2.5、-2.5对应点到-1、1对应点的距离之和正好等于5,
故原不等式的解集为{x|x<-2.5,或x>2.5},
故答案为:{x|x<-2.5,或x>2.5}.
点评 本题主要考查绝对值不等式的解法,绝对值的意义,体现了分类讨论、转化的数学思想,属于中档题.

练习册系列答案
相关题目
6.△ABC是边长为1的正三角形,PA⊥平面ABC,且PA=$\frac{\sqrt{6}}{4}$,点A关于平面PBC的对称点为A′,则异面直线A′C与AB所成角等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
10.已知函数f(x)=x3-bx2-4,x∈R,则下列命题正确的是( )
| A. | 当b>0时,?x0<0,使得f(x0)=0 | |
| B. | 当b<0时,?x<0,都有f(x)<0 | |
| C. | f(x)有三个零点的充要条件是b<-3 | |
| D. | f(x)在区间(0.+∞)上有最小值的充要条件是b<0 |
2.已知集合A={x|x2-2x-3≤0},B={y|y=x2,x∈R},则A∩B=( )
| A. | ∅ | B. | [0,1] | C. | [0,3] | D. | [-1,+∞) |
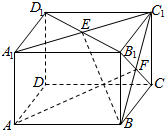 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.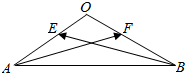 等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.