题目内容
14.如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2$\sqrt{2}$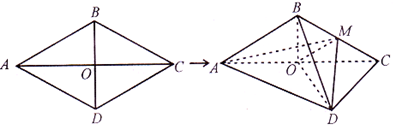
(I)求证:OD⊥平面ABC;
(Ⅱ)求直线MD与平面ABD所成角的正弦.
分析 (Ⅰ)只需证明OD⊥AC,DO⊥OM,即可证得OD⊥面ABC.
(Ⅱ)设M到平面ABD的距离为h,直线MD与平面ABD所成的角为α
由VM-ADB=VD-ABM求出h,即sin$α=\frac{h}{MD}$即可
解答 解:(Ⅰ)证明:∵ABCD是菱形,AD=DC,OD⊥AC …(1分)
△ADC中,AD=DC=4,∠ADC=120°,∴OD=2,
又M是DC中点,$OM=OD=2,DM=2\sqrt{2}$,∵OD2+OM2=MD2,∴DO⊥OM…(4分)
OM,AC?面ABC,OM∩AC=0,∴OD⊥面ABC …(6分)
(Ⅱ)△ABM中,AB=4,BM=2,∠ABM=120°
s△ABM=$\frac{1}{2}AB•BM•sin12{0}^{0}$=2$\sqrt{3}$
由(Ⅰ)得OD⊥面ABC
∴VM-ADB=VD-ABM=$\frac{1}{3}OD•{s}_{△ABM}$=$\frac{{4\sqrt{3}}}{3}…(8分)$.
设M到平面ABD的距离为h,直线MD与平面ABD所成的角为α.
∵$AB=4,AD=4,可知BD=2\sqrt{2}$,∴A到DB的距离d=$\sqrt{{4}^{2}-(\sqrt{2})^{2}}$=$\sqrt{14}$.
∴${s}_{△ADB}=\frac{1}{2}×2\sqrt{2}×\sqrt{14}=2\sqrt{7}$
∴VM-ADB=$\frac{1}{3}{s}_{ADB}×h$=$\frac{1}{3}×2\sqrt{7}×h=\frac{4\sqrt{3}}{3}$
∴$h=\frac{2\sqrt{21}}{7}$,即sin$α=\frac{h}{MD}$=$\frac{\sqrt{42}}{14}$
∴直线MD与平面ABD所成角的正弦为$\frac{\sqrt{42}}{14}$.
点评 本题考查了空间线面垂直的判定,几何法求线面角,等体积法求点面距离,属于中档题.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | $\frac{2}{81}$ | B. | $\frac{4}{27}$ | C. | $\frac{8}{27}$ | D. | $\frac{16}{81}$ |
| A. | 3 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| A. | 45 | B. | 50 | C. | 55 | D. | 60 |

| A. | 0<a<1,b>0 | B. | 0<a<1,b<0 | C. | a>1,b<0 | D. | a>1,b>0 |