题目内容

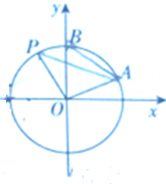如图，一个半径为R的圆上一点A（
3
，1），动点P从点A出发，沿圆周按逆时针方向匀速运动，设t时刻时，P点坐标为（x（t），y（t）），其中t∈[2，6]时，y（t）单调递减，且y（6）=y（10），则0≤t≤10时，数量积
AP
•
AB
的最大值为（　　）
A、4B、6C、10D、12
考点：平面向量数量积的运算
专题：计算题,三角函数的图像与性质,平面向量及应用
分析：由A的坐标，求得R=2，运用三角函数的定义可得P的坐标P（2cos（
π
6
+ωt），2sin（
π
6
+ωt）），（θ=ωt），再由条件求出ω，再根据向量的数量积的坐标表示化简整理，由正弦函数的图象和性质，计算即可得到最大值．
解答： 解：由于A（
3
，1），则∠AOx=
π
6
，R=2，B（0，2），
设t时刻时旋转了θ角，则P（2cos（
π
6
+ωt），2sin（
π
6
+ωt）），（θ=ωt），
由于y（6）=y（10），
即2sin（
π
6
+6ω）=2sin（
π
6
+10ω），
即
π
6
+6ω=
π
6
+10ω+2kπ或
π
6
+6ω+
π
6
+10ω=2kπ+π（k∈Z），
ω=-
kπ
2
或ω=
kπ
8
+
π
24
，
由t∈[2，6]时，y（t）单调递减，
则k=1时，ω=
π
8
+
π
24
=
π
6
，
则有P（（2cos（
π
6
+
π
6
t），2sin（
π
6
+
π
6
t）），
则
AP
=（2cos（
π
6
+
π
6
t）-
3
，2sin（
π
6
+
π
6
t）-1），
AB
=（-
3
，1），
即有
AP
•
AB
=2-2
3
cos（
π
6
+
π
6
t）+2sin（
π
6
+
π
6
t）
=2+4sin（
π
6
+
π
6
t-
π
3
）=2+4sin（
π
6
t-
π
6
），
当0≤t≤10时，-
π
6
≤
π
6
t-
π
6
≤
3π
2
，
则有-1≤sin（
π
6
t-
π
6
）≤1，
则有-2≤
AP
•
AB
≤6．
则最大值为6．
故选：B．
点评：本题主要考查三角函数的定义和性质，以及平面向量的数量积运算，要求熟练掌握三角函数的图象和性质，考查学生的运算能力．
练习册系列答案
相关题目
化简：cos2（
2π
3
+α）+cos2（
7π
6
+α）
2014年10月20日，国务院发布《关于加快发展体育产业促进体育消费的若干意见》，要求切实保障中小学体育课课时，鼓励实施课外体育活动计划，培养青少年体育爱好．某校为此在周一安排篮球、周三安排排球、周五安排足球，共三次集体活动，根据统计，某班每名学生参加这三次活动的概率分别为
3
4
、
1
3
、
1
2
，并且报名参加三次活动之间互不影响．
（1）现有该班甲、乙、丙、丁4名学生，求这4名学生中至少有3名报名参加篮球活动的概率；
（2）若用X表示该班学生甲报名参加集体活动的次数，求X的分布列与数学期望．
四棱锥的三视图如图所示，则最长的一条侧棱的长度是（　　）
A、
29
B、5
C、
13
D、2
2
大学毕业的小张到甲、乙、丙三个不同的单位应聘，各单位是否录用他相互独立，其被录用的概率分别为
4
5
、
3
4
、
2
3
（允许小张被多个单位同时录用）
（1）小张没有被录用的概率；
（2）设录用小张的单位个数为ξ，求ξ的分布列和它的数学期望．
已知△ABC，P0是边AB上一定点，满足
P0B
=
1
4
AB
，且对于AB上任一点P，恒有
PB
•
PC
≥
P0B
•
P0C
．若A=
π
3
，|
AC
|=2，则△ABC的面积为
 
．
已知函数f（x）=（x+2a）|x-a|+x，a∈R．
（1）当a=0时，判断函数y=f（x）的奇偶性，并加以证明；
（2）若对任意的x∈[-2，2]，函数f（x）图象恒在函数g（x）=（2a+1）x+4a2的图象的下方，求实数a的取值范围．
下列函数中，既是偶函数又在区间（0，+∞）上递增的函数为（　　）
A、y=x3
B、y=|log2x|
C、y=-x2
D、y=|x|
设a，b是夹角为30°的异面直线，则满足条件“a⊆α，b⊆β，且α⊥β”的平面α，β（　　）
A、不存在B、有且只有一对
C、有且只有两对D、有无数对

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网